
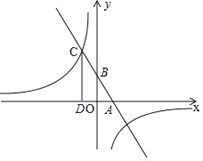
【题目】已知,如图,一次函数y=kx+b(k、b为常数且k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() ,m为常数且m≠0)的图象在第二象限交于点C.若CD⊥x轴于D,若OA=OD=2,cos∠BAO=
,m为常数且m≠0)的图象在第二象限交于点C.若CD⊥x轴于D,若OA=OD=2,cos∠BAO=![]() .
.
(1)求一次函数与反比例函数的解析式.
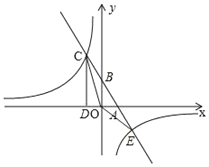
(2)若一次函数与反比例函数的另一个交点坐标为E,连接OC、OE,求△COE面积.
【答案】(1)y=-![]() ,y=﹣
,y=﹣![]() x+3(2)9
x+3(2)9
【解析】
(1)根据OA=OD=2,cos∠BAO=![]() 和勾股定理,求得C(﹣2,6),把C(﹣2,6)代入反比例函数y=
和勾股定理,求得C(﹣2,6),把C(﹣2,6)代入反比例函数y=![]() ,可得反比例函数的解析式,把C(﹣2,6),A(2,0)代入一次函数y=kx+b,即可得一次函数解析式;
,可得反比例函数的解析式,把C(﹣2,6),A(2,0)代入一次函数y=kx+b,即可得一次函数解析式;
(2)先求得一次函数与y轴的B的坐标,再根据反比例函数的解析式和一次函数解析式求出交点E的坐标,再根据S△COE=S△COB+S△EOB进行计算即可.
(1)在Rt△ACD中,
∵OA=OD=2,cos∠BAO=![]() =
=![]() ,
,
∴AC=2![]() ,AD=4,
,AD=4,
∴Rt△ACD中,CD=![]() =6,
=6,
∴C(﹣2,6),
把C(﹣2,6)代入反比例函数y=![]() ,可得
,可得
m=﹣12,
∴反比例函数的解析式为y=﹣![]() .
.
把C(﹣2,6),A(2,0)代入一次函数y=kx+b,
可得![]() ,解得
,解得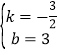
∴一次函数解析式为y=﹣![]() x+3;
x+3;
(2)y=﹣![]() x+3中,令x=0,则y=3,即B(0,3),
x+3中,令x=0,则y=3,即B(0,3),
解方程组 ,可得
,可得![]() ,
,![]() ,
,
∴E(4,﹣3),
∴S△COE=S△COB+S△EOB
=![]() ×3×(2+4)
×3×(2+4)
=9.


科目:初中数学 来源: 题型:
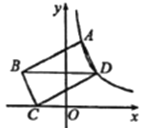
【题目】如图,在平面直角坐标系中,平行四边形![]() 的顶点
的顶点![]() 在反比例函数
在反比例函数![]() (
(![]() )的图象上,点
)的图象上,点![]() 在
在![]() 轴上,对角线
轴上,对角线![]() 轴,若
轴,若![]() 两点的横坐标分别为1,2,
两点的横坐标分别为1,2,![]() 的长为
的长为![]() ,则
,则![]() 的值为____.
的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,过点A(﹣![]() ,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根
,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根
(1)求线段BC的长度;
(2)试问:直线AC与直线AB是否垂直?请说明理由;
(3)若点D在直线AC上,且DB=DC,求点D的坐标;
(4)在(3)的条件下,直线BD上是否存在点P,使以A、B、P三点为顶点的三角形是等腰三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
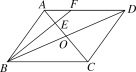
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() =
=![]() ;②S△BCE=36;③S△ABE=12;④△AEF∽△ACD,其中正确结论是_________.(把正确结论的序号都填上)
;②S△BCE=36;③S△ABE=12;④△AEF∽△ACD,其中正确结论是_________.(把正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
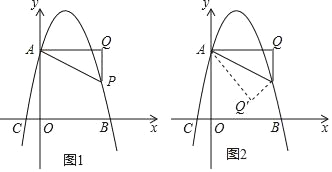
【题目】如图1,已知抛物线y=﹣x2+bx+c交y轴于点A(0,4),交x轴于点B(4,0),点P是抛物线上一动点,过点P作x轴的垂线PQ,过点A作AQ⊥PQ于点Q,连接AP.
(1)填空:抛物线的解析式为 ,点C的坐标 ;
(2)点P在抛物线上运动,若△AQP∽△AOC,求点P的坐标;
(3)如图2,当点P位于抛物线的对称轴的右侧,若将△APQ沿AP对折,点Q的对应点为点Q',请直接写出当点Q'落在坐标轴上时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD;请证明你的结论.

【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,有一Rt△ABC,且A(﹣1,3),B(﹣3,﹣1),C(﹣3,3),已知△A1AC1是由△ABC旋转得到的.
(1)请写出旋转中心的坐标是 ,旋转角是 度;
(2)以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°、180°的三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图的名称;

视图 视图
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com