
【题目】如图 , ![]() 中,
中, ![]() ,线段
,线段![]() 在射线
在射线![]() 上,且
上,且![]() ,线段
,线段![]() 沿射线
沿射线![]() 运动,开始时,点
运动,开始时,点![]() 与点
与点![]() 重合,点
重合,点![]() 到达点
到达点![]() 时运动停止,过点
时运动停止,过点![]() 作
作![]() ,与射线
,与射线![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 的垂线,与射线
的垂线,与射线![]() 相交于点
相交于点![]() .设
.设![]() ,四边形
,四边形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() 关于
关于![]() 的函数图象如图所示(其中
的函数图象如图所示(其中![]() 时,函数的解析式不同)
时,函数的解析式不同)
(1)填空: ![]() 的长是 ;
的长是 ;
(2)求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围.
的取值范围.

【答案】(1)6;(2)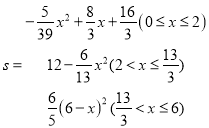
【解析】试题分析:(1)由图象即可解决问题.
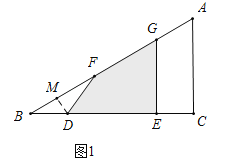
(2)分三种情形①如图1中,当0≤x≤2时,作DM⊥AB于M,根据S=S△BEG﹣S△BDF即可解决.
②如图2中,作AN∥DF交BC于N,设BN=AN=x.在Rt△ANC中,利用勾股定理求出x,再根据S= S△ABC﹣S△BDF即可解决.
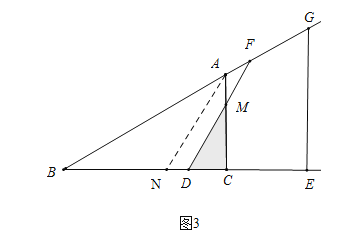
③如图3中,根据S=![]() CDCM,求出CM即可解决问题.
CDCM,求出CM即可解决问题.
试题解析:解;(1)由图象可知BC=6.故答案为:6.
(2)①如图1中,当0≤x≤2时,作DM⊥AB于M,由题意BC=6,AC=4,∠C=90°,∴AB=![]() =
=![]() .∵∠B=∠B,∠DMB=∠C=90°,∴△BMD∽△BCA,∴
.∵∠B=∠B,∠DMB=∠C=90°,∴△BMD∽△BCA,∴![]() ,∴DM=
,∴DM=![]() ,BM=
,BM=![]() .∵BD=DF,DM⊥BF,∴BM=MF,∴S△BDF=
.∵BD=DF,DM⊥BF,∴BM=MF,∴S△BDF=![]() .∵EG∥AC,∴
.∵EG∥AC,∴![]() ,∴
,∴![]() ,∴EG=
,∴EG=![]() (x+4),∴S=S△BEG﹣S△BDF=
(x+4),∴S=S△BEG﹣S△BDF=![]() =
=![]() .
.
②如图②中,作AN∥DF交BC于N,设BN=AN=x.在Rt△ANC中,∵AN2=CN2+AC2,∴x2=42+(6﹣x)2,∴x=![]() ,∴当2<x≤
,∴当2<x≤![]() 时,S=S△ABC﹣S△BDF=12﹣
时,S=S△ABC﹣S△BDF=12﹣![]() ;
;

③如图3中,当![]() <x≤6时.∵DM∥AN,∴
<x≤6时.∵DM∥AN,∴![]() ,∴
,∴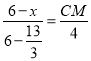 ,∴CM=
,∴CM=![]() (6﹣x),∴S=
(6﹣x),∴S=![]() CDCM=
CDCM=![]() .
.
综上所述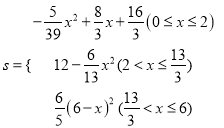 .
.


科目:初中数学 来源: 题型:
【题目】国家自2016年1月1日起实行全面放开二胎政策,某计生组织为了解该市家庭对待这项政策的态度,准备采用以下调查方式中的一种进行调查:
A.从一个社区随机选取1 000户家庭调查;
B.从一个城镇的不同住宅楼中随机选取1 000户家庭调查;
C.从该市公安局户籍管理处随机抽取1 000户城乡家庭调查.
(1)在上述调查方式中,你认为比较合理的一个是【1】.(填“A”、“B”或“C”)
(2)将一种比较合理的调查方式调查得到的结果分为四类:(A)已有两个孩子;
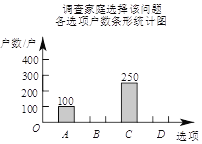
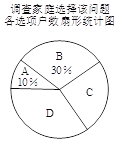
(B)决定生二胎;(C)考虑之中;(D)决定不生二胎.将调查结果绘制成如下两幅不完整的统计图.
请根据以上不完整的统计图提供的信息,解答下列问题:
①补全条形统计图.
②估计该市100万户家庭中决定不生二胎的家庭数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班同学为了解2019年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行整理如下:
月均用水量x(t) | 频数(户) | 频率 |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
| 2 | 0.04 |

请解答下列问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期五晚上,小明和他的妈妈一起看《歌手》,歌手演唱完后要评选出名次,在已公布四到七名后,还有华晨宇、汪峰、张韶涵三位选手没有公布名次.
(1)求汪峰获第一名的概率;
(2)如果小明和妈妈一起竞猜第一名,那么两人中一个人猜中另一个人却没猜中的概率是多少?(请用“树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两地在数轴上相距20米,A地在数轴上表示的点为-8,小乌龟从A地出发沿数轴往B地方向前进,第一次前进1米,第二次后退2米,第三次再前进3米,第四次又后退4米,……,按此规律行进,(数轴的一个单位长度等于1米)
![]()
(1)求B地在数轴上表示的数;
(2)若B地在原点的左侧,经过第五次行进后小乌龟到达点P,第六次行进后到达点Q,则点P和点Q到点A的距离相等吗?请说明理由;
(3)若B地在原点的右侧,那么经过30次行进后,小乌龟到达的点与点B之间的距离是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用三种大小不同的五个正方形和一个缺角的长方形拼成长方形 ABCD,其中,NH=NG 1cm ,设 BF acm .
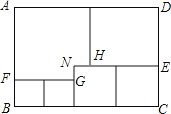
(1)用含 a 的代数式分别表示 CE,DE;
(2)求长方形 ABCD 的周长.(用含 a 的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,四边形OABC为矩形,A(6,0),C(0,3),点M在边OA上,且M(4,0),P、Q两点同时从点M出发,点P沿x轴向右运动;点Q沿x轴先向左运动至原点O后,再向右运动到点M停止,点P随之停止运动.P、Q两点运动的速度分别为每秒1个单位、每秒2个单位.以PQ为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与矩形OABC重叠部分(阴影部分)的面积为S(平方单位).
(1)用含t的代数式表示点P的坐标.
(2)分别求当t=1,t=3时,线段PQ的长.
(3)求S与t之间的函数关系式.
(4)直接写出L落在第一象限的角平分线上时t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)图(1)是一个长为2m,宽为2n的矩形,把此矩形沿图中虚线用剪刀均分为四个小长方形,然后按图(2)的形状拼成一个大正方形.请问:这两个图形的什么量不变?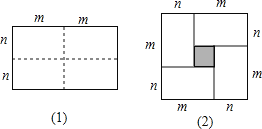
(2)把所得的大正方形面积比原矩形的面积多出的阴影部分的面积用含m,n的代数式表示为(m-n)2或m2-2mn+n2 .
(3)由前面的探索可得出的结论是:在周长一定的矩形中,当 时,面积最大.
(4)若矩形的周长为24cm,则当边长为多少时,该图形的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
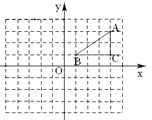
【题目】如图,网格中的每个小正方形的边长均为1个单位长度,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A(4,3),点B(1,1),点C(4,1).
(1)画出Rt△ABC关于y轴对称的Rt△A1B1C1,(点A、B、C的对称点分别是A1、B1、C1),直接写出A1的坐标;
(2)将Rt△ABC向下平移4个单位,得到Rt△A2B2C2(点A、B、C的对应点分别是A2、B2、C2),画出Rt△A2B2C2 ,连接A1C2,直接写出线段A1C2的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com