
【题目】如图,公交车行驶在笔直的公路上,这条路上有![]() ,
,![]() ,
,![]() ,
,![]() 四个站点,每相邻两站之间的距离为5千米,从
四个站点,每相邻两站之间的距离为5千米,从![]() 站开往
站开往![]() 站的车称为上行车,从
站的车称为上行车,从![]() 站开往
站开往![]() 站的车称为下行车.第一班上行车、下行车分别从
站的车称为下行车.第一班上行车、下行车分别从![]() 站、
站、![]() 站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在
站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在![]() ,
,![]() 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.
站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.

(1)问第一班上行车到![]() 站、第一班下行车到
站、第一班下行车到![]() 站分别用时多少?
站分别用时多少?
(2)若第一班上行车行驶时间为![]() 小时,第一班上行车与第一班下行车之间的距离为
小时,第一班上行车与第一班下行车之间的距离为![]() 千米,求
千米,求![]() 与
与![]() 的函数关系式.
的函数关系式.
(3)一乘客前往![]() 站办事,他在
站办事,他在![]() ,
,![]() 两站间的
两站间的![]() 处(不含
处(不含![]() ,
,![]() 站),刚好遇到上行车,
站),刚好遇到上行车,![]() 千米,此时,接到通知,必须在35分钟内赶到,他可选择走到
千米,此时,接到通知,必须在35分钟内赶到,他可选择走到![]() 站或走到
站或走到![]() 站乘下行车前往
站乘下行车前往![]() 站.若乘客的步行速度是5千米/小时,求
站.若乘客的步行速度是5千米/小时,求![]() 满足的条件.
满足的条件.
【答案】(1)第一班上行车到![]() 站用时
站用时![]() 小时,第一班下行车到
小时,第一班下行车到![]() 站用时
站用时![]() 小时;(2)当
小时;(2)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】(1)根据速度=路程除以时间即可求出第一班上行车到![]() 站、第一班下行车到
站、第一班下行车到![]() 站的用时.
站的用时.
(2)分当![]() 时和当
时和当![]() 时两种情况进行讨论.
时两种情况进行讨论.
(3)由(2)知同时出发的一对上、下行车的位置关于![]() 中点对称,设乘客到达
中点对称,设乘客到达![]() 站总时间为
站总时间为![]() 分钟,分当
分钟,分当![]() 时,当
时,当![]() 时,当
时,当![]() 时,三种情况进行讨论.
时,三种情况进行讨论.
【解答】(1)第一班上行车到![]() 站用时
站用时![]() 小时.
小时.
第一班下行车到![]() 站用时
站用时![]() 小时.
小时.
(2)当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() .
.
(3)由(2)知同时出发的一对上、下行车的位置关于![]() 中点对称,设乘客到达
中点对称,设乘客到达![]() 站总时间为
站总时间为![]() 分钟,
分钟,
当![]() 时,往
时,往![]() 站用时30分钟,还需再等下行车5分钟,
站用时30分钟,还需再等下行车5分钟,
![]() ,不合题意.
,不合题意.
当![]() 时,只能往
时,只能往![]() 站坐下行车,他离
站坐下行车,他离![]() 站
站![]() 千米,则离他右边最近的下行车离
千米,则离他右边最近的下行车离![]() 站也是
站也是![]() 千米,这辆下行车离
千米,这辆下行车离![]() 站
站![]() 千米.
千米.
如果能乘上右侧第一辆下行车,![]() ,
,![]() ,∴
,∴![]() ,
,
![]() ,
,
∴![]() 符合题意.
符合题意.
如果乘不上右侧第一辆下行车,只能乘右侧第二辆下行车,![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 符合题意.
符合题意.
如果乘不上右侧第二辆下行车,只能乘右侧第三辆下行车,![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,![]() ,不合题意.
,不合题意.
∴综上,得![]() .
.
当![]() 时,乘客需往
时,乘客需往![]() 站乘坐下行车,
站乘坐下行车,
离他左边最近的下行车离![]() 站是
站是![]() 千米,
千米,
离他右边最近的下行车离![]() 站也是
站也是![]() 千米,
千米,
如果乘上右侧第一辆下行车,![]() ,
,
∴![]() ,不合题意.
,不合题意.
如果乘不上右侧第一辆下行车,只能乘右侧第二辆下行车,![]() ,
,
![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() 符合题意.
符合题意.
如果乘不上右侧第二辆下行车,只能乘右侧第三辆下行车,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
∴![]() 不合题意.
不合题意.
∴综上,得![]() .
.
综上所述,![]() 或
或![]() .
.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知整数a1,a2,a3,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…依此类推,则a2020的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
(1)求证:直线CE是⊙O的切线.
(2)若BC=3,CD=3![]() ,求弦AD的长.
,求弦AD的长.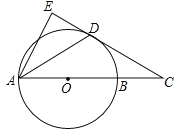
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线![]() ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() )
)
例2 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() 或
或![]() 或
或![]() )
)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.
的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,![]() 的度数不同,得到
的度数不同,得到![]() 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形![]() 中,设
中,设![]() ,当
,当![]() 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校检测学生跳绳水平,抽样调查了部分学生的“一分钟跳绳”成绩,并绘制了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图.
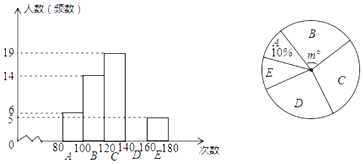
(1)抽样的人数是________人,补全频数分布直方图,扇形中![]() ________;
________;
(2)本次调查数据的中位数落在________组;
(3)如果“一分钟跳绳”成绩大于等于120次为优秀,那么该校2250名学生中“1分钟跳绳”成绩为优秀的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC与BD交于点O,E是BD上一点,EF//AB,∠EAB=∠EBA,过点B作DA的垂线,交DA的延长线于点G.
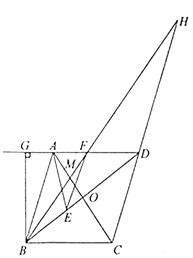
(1)∠DEF和∠AEF是否相等?若相等,请证明;若不相等,请说明理由;
(2)找出图中与ΔAGB相似的三角形,并证明;
(3)BF的延长线交CD的延长线于点H,交AC于点M.求证:BM2=MFMH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点F,D,E分别是边AB,BC,AC上的点,且AD,BE,CF相交于点O,若点O是△ABC的重心,则以下结论:①线段AD,BE,CF是△ABC的三条角平分线;②△ABD的面积是△ABC面积的一半;③图中与△ABD面积相等的三角形有5个;④△BOD的面积是△ABD面积的![]() ;⑤AO=2OD其中一定正确结论有( )
;⑤AO=2OD其中一定正确结论有( )
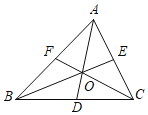
A.①③④⑤B.②③④⑤C.③④⑤D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com