
【题目】某班为参加学校的大课间活动比赛,准备购进一批跳绳,已知2根A型跳绳和1根B型跳绳共需56元,1根A型跳绳和2根B型跳绳共需82元.
(1)求一根A型跳绳和一根B型跳绳的售价各是多少元?
(2)学校准备购进这两种型号的跳绳共50根,并且A型跳绳的数量不多于B型跳绳数量的3倍,请设计书最省钱的购买方案,并说明理由.
【答案】
(1)解:设一根A型跳绳售价是x元,一根B型跳绳的售价是y元,
根据题意,得:
![]() ,
,
解得: ![]() ,
,
答:一根A型跳绳售价是10元,一根B型跳绳的售价是36元;
(2)解:设购进A型跳绳m根,总费用为W元,
根据题意,得:W=10m+36(50﹣m)=﹣26m+1800,
∵﹣26<0,
∴W随m的增大而减小,
又∵m≤3(50﹣m),解得:m≤37.5,
而m为正整数,
∴当m=37时,W最小=﹣2×37+350=276,
此时50﹣37=13,
答:当购买A型跳绳37只,B型跳绳13只时,最省钱.
【解析】(1)设一根A型跳绳售价是x元,一根B型跳绳的售价是y元,根据:“2根A型跳绳和1根B型跳绳共需56元,1根A型跳绳和2根B型跳绳共需82元”列方程组求解即可;(2)首先根据“A型跳绳的数量不多于B型跳绳数量的3倍”确定自变量的取值范围,然后得到有关总费用和A型跳绳之间的关系得到函数解析式,确定函数的最值即可.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
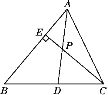
【题目】如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD、CE相交于点P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E为AD的中点,请只用无刻度的直尺作图
(1)如图1,在BC上找点F,使点F是BC的中点;
(2)如图2,在AC上取两点P,Q,使P,Q是AC的三等分点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角尺如图①摆放(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°).点D为AB的中点,DE交AC于点P,DF经过点C. 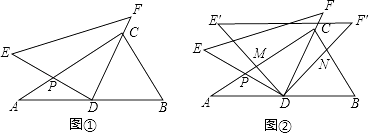
(1)求∠ADE的度数;
(2)如图②,在图①的基础上将△DEF绕点D顺时针方向旋转角α(0°<α<60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,求证: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使三角形AMN周长最小时,则∠AMN+∠ANM的度数为( )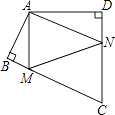
A.80°
B.90°
C.100°
D.130°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D。AF平分∠CAB,交CD于点E,交CB于点F。

(1)求证:CE=CF。
(2)将图(1)中的△ADE沿AB向右平移到△A′D′E′的位置,使点E′落在BC边上,其它条件不变,如图(2)所示。试猜想:BE′与CF有怎样的数量关系?请证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为 ![]() ,点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值为( )
,点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值为( )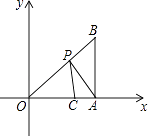
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一张△ABC纸片,点D,E分别在线段AC,AB上,将△ADE沿着DE折叠,A与A′重合,若∠A=α,则∠1+∠2=( ) 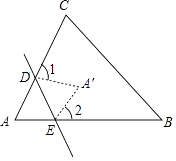
A.α
B.2α
C.180°﹣α
D.180°﹣2α
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com