
����Ŀ����ֱ֪��l����һ��O����A��Bͬʱ��O��������ֱ��l�Ϸֱ����������������˶�����A��B���ٶȱ�Ϊ1��2�����˶�ʱ��Ϊts��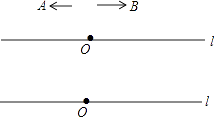
��1����t=2sʱ��AB=12cm����ʱ��
����ֱ��l�ϻ���A��B�����˶�2��ʱ��λ�ã����ش��A�˶����ٶ���cm/s�� ��B�˶����ٶ���cm/s��
������PΪֱ��l��һ�㣬��PA��PB=OP���� ![]() ��ֵ��
��ֵ��
��2���ڣ�1���������£���A��Bͬʱ��ԭ�������˶����پ������룬OA=2OB��
���𰸡�
��1��2,4,�⣺��ͼ2,��P��AB֮��ʱ,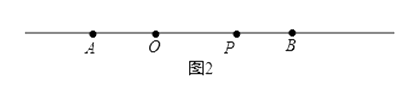 ��PA��OA=OP,PA��PB=OP,��PA��OA=PA��PB,��OA=PB=4,��OP=4����
��PA��OA=OP,PA��PB=OP,��PA��OA=PA��PB,��OA=PB=4,��OP=4���� ![]() ����ͼ3,��P��AB���Ҳ�ʱ,
����ͼ3,��P��AB���Ҳ�ʱ, ��PA��OA=OP,PA��PB=OP, ��PA��OA=PA��PB, ��OA=PB=4,��OP=12����
��PA��OA=OP,PA��PB=OP, ��PA��OA=PA��PB, ��OA=PB=4,��OP=12���� ![]() ��
�� ![]() =
= ![]() ��1
��1
��2���⣺��A��Bͬʱ��ԭ�������˶����پ�����a��OA=2OB�������⣬��
2a+4=2��8��4a����2a+4=2��4a��8��
��ã�a= ![]() ��
�� ![]()
���پ��� ![]() ��
�� ![]() ��ʱOA=2OB��
��ʱOA=2OB��
���������⣺��1������ͼ��ʾ��
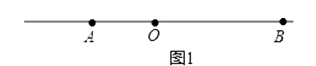
��A���ٶ�Ϊxcm/s��B���ٶ�Ϊ2xcm/s�������⣬��
2x+4x=12��
��ã�x=2��
��B���ٶ�Ϊ4cm/s��
�ʴ�Ϊ��2��4
��1������A���ٶ�Ϊxcm/s��B���ٶ�Ϊ2xcm/s������2s���ľ���Ϊ12�������������⼴�ɣ�
�ڷ����������ͼ2�� ��P��AB֮��ʱ������PA��OA=OP��PA��PB=OP ���ó�OA=PB=4�������߶εĺͲ�ó�OP=4 ���Ӷ��ó���OP��AB��ֵ����ͼ3����P��AB���Ҳ�ʱ����PA��OA=OP��PA��PB=OP���ó�OA=PB=4�������ó�OP=12 ���Ӷ��ó�OP��AB��ֵ ��
��2����A��Bͬʱ��ԭ�������˶����پ�����a��OA=2OB�������������������ϵ��������2a+4=2��8��4a����2a+4=2��4a��8�� �����⼴�ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
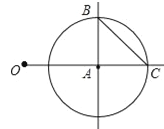
����Ŀ����ͼ��OA=2���Ե�AΪԲ�ģ�1Ϊ�뾶����A��OA���ӳ��߽��ڵ�C������A��OA�Ĵ��ߣ��������A��һ������ΪB������BC
��1���߶�BC�ij����� ��
��2������ͼ�а�����Ҫ����һ���������ش����⣺
���Ե� ΪԲ�ģ����߶� �ij�Ϊ�뾶������������BA���ڵ�D��ʹ�߶�OD�ij�����![]() ��
��
����OD����OD�ϻ�����P��ʹOP�ó�����![]() ����д����������˵�����ɣ�
����д����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ⶳ�Ρ���üɽ������ɫС�ԣ���Ʒ����ʡ���⣬����һ����Ʒ���۵��ھ���ʱ���֣����ÿ���Ʒӯ��10Ԫ��ÿ����۳�50�䣻��ÿ���Ʒ�Ǽ�1Ԫ����������������2�䣮
��1���ָ����۵�ÿ��ӯ��600Ԫ��ͬʱ��Ҫ�˿͵õ�ʵ�ݣ���ôÿ���ƷӦ�Ǽ۶���Ԫ��
��2���������۵㵥���Ӿ��ýǶȿ��ǣ�ÿ���ƷӦ�Ǽ۶���Ԫ���ܻ�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ�Ǽ�30%�����ָ�ԭ�ۣ�������½��İٷ���ԼΪ�� ��
A.20%
B.21%
C.22%
D.23%
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y��x2��4x+m��ͼ�����������㣨��3��y1������1��y2������4��y3������y1��y2��y3�Ĵ�С��ϵΪ��������
A.y2��y3��y1B.y1��y2��y3C.y1��y2��y3D.y3��y2��y1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ԡ�AOB�Ķ���OΪԲ�ģ��ʵ���Ϊ�뾶��������OA�ڵ�C����OB�ڵ�D���ٷֱ��Ե�C��DΪԲ�ģ����� ![]() CD�ij�Ϊ�뾶�����������ڡ�AOB�ڲ����ڵ�E������E������OE������CD��������˵��������ǣ� ��
CD�ij�Ϊ�뾶�����������ڡ�AOB�ڲ����ڵ�E������E������OE������CD��������˵��������ǣ� �� 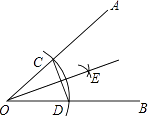
A.����OE�ǡ�AOB��ƽ����
B.��COD�ǵ���������
C.O��E�������CD����ֱ�߶Գ�
D.C��D�������OE����ֱ�߶Գ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����OΪֱ��AB��һ�㣬����O������OC��ʹ��BOC=120�㣮��һֱ�����ǰ��ֱ�Ƕ�����ڵ�O����һ��OM������OB�ϣ���һ��ON��ֱ��AB���·���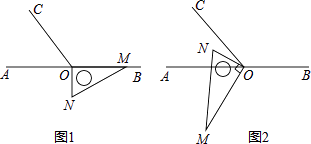
��1����ͼ1�е����ǰ��Ƶ�O��ÿ��10����ٶ�����ʱ�뷽����תһ�ܣ�����ת�Ĺ����У������t��ʱ��OA��OC��ON�������߹�����ȵĽǣ����ʱt��ֵΪ���٣�
��2����ͼ1�е����ǰ��Ƶ�O˳ʱ����תͼ2��ʹON�ڡ�AOC���ڲ�����̽������AOM���NOC֮���������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��NBA��������У�Ҧ����Ͷ��a��2����b��3����ͨ������õ�9�֣����ⳡ�����У���һ������____________�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������AOBƽ������һ��C��CD��OB��OA�ڵ�D��E���߶�OC���е㣬�����E��ֱ�߷ֱ�����CD��OB�ڵ�M��N��̽���߶�OD��ON��DM֮���������ϵ����֤����Ľ��ۣ�
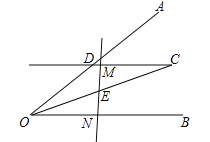
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com