
分析 先画树状图展示12种等可能的结果数,再根据根的判别式得到使二次方程x2+ax+b=0无实根的结果数,然后根据概率公式求解.
解答 解:画树状图为:
共有12种等可能的结果数,其中使二次方程x2+ax+b=0无实根的有a=-1,b=1;a=-1,b=2;a=0,b=1;a=0,b=2;a=1,b=2),
所以使二次方程x2+ax+b=0无实根的概率=$\frac{5}{12}$.
故答案为$\frac{5}{12}$
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了根的判别式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x}$ | B. | y=-$\frac{1}{x}$ | C. | y=$\frac{2}{x}$ | D. | y=-$\frac{2}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
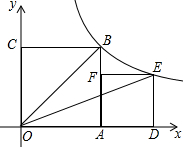 如图,两个正方形OABC、ADEF拼放于直角坐标系中,反比例函数y=$\frac{k}{x}(k≠0,x>0)$的图象经过B点和E点,已知△OEB的面积为2,则正方形ADEF的面积为( )
如图,两个正方形OABC、ADEF拼放于直角坐标系中,反比例函数y=$\frac{k}{x}(k≠0,x>0)$的图象经过B点和E点,已知△OEB的面积为2,则正方形ADEF的面积为( )| A. | 1 | B. | 6-2$\sqrt{5}$ | C. | $\sqrt{5}-1$ | D. | 3$\sqrt{5}$-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
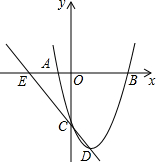 如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,-3).
如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,-3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
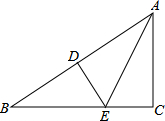 如图,DE是△ABC的AB边的垂直平分线,分别交AB、BC于点D、E,AE平分∠BAC,∠C=90°,则∠B的度数为( )
如图,DE是△ABC的AB边的垂直平分线,分别交AB、BC于点D、E,AE平分∠BAC,∠C=90°,则∠B的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com