
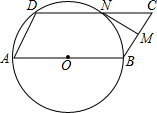
 如图,平行四边形ABCD中,AB=2,∠A=60°,以AB为直径的⊙O过点D,点M是BC边上一点(点M不与B,C重合),过点M作BC的垂线MN,交CD边于点N.
如图,平行四边形ABCD中,AB=2,∠A=60°,以AB为直径的⊙O过点D,点M是BC边上一点(点M不与B,C重合),过点M作BC的垂线MN,交CD边于点N.分析 (1)连接OD,由题意证出△AOD是等边三角形,得出AD=OA=1即可;
(2)连接ON,由平行四边形的性质得出AB∥CD,BC=AD=1,∠C=∠A=60°,证出△DON是等边三角形,得出∠DNO=60°,求出∠CNM=30°,因此∠ONM=90°即可;
(3)①由含30°角的直角三角形的性质得出CN=2CM,即可得出结果;
②作PE⊥AB于E,CN⊥AB于N,则∠BCN=30°,由含30°角的直角三角形的性质得出BN=$\frac{1}{2}$BC=$\frac{1}{2}$,得出PE=CN=$\frac{\sqrt{3}}{2}$,由相切两圆的圆心距=两圆半径之和,得出OP=OB+PC=2-x,因此OE=OB+BN-EN=$\frac{1}{2}$+x,由勾股定理得出方程,解方程即可.
解答 (1)解: 连接OD,如图1所示:
连接OD,如图1所示:
根据题意得:OA=OB=1,
∵OA=OD,∠A=60°,
∴△AOD是等边三角形,
∴AD=OA=1,∠AOD=60°;
(2)证明:连接ON,如图2所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,BC=AD=1,∠C=∠A=60°,
∴∠ODN=∠AOD=60°,
∵OD=ON,
∴△DON是等边三角形,
∴∠DNO=60°,
∵MN⊥BC,
∴∠CNM=90°-60°=30°,
∴∠ONM=180°-30°-60°=90°,
即MN⊥ON,
∴直线MN是⊙O的切线;
(3)解:①∵∠CNM=30°,MN⊥BC,
∴CN=2CM,即y=2(1-x),
∴y=2-2x,
即y关于x的函数关系式为y=2-2x(0<x<1);
②作PE⊥AB于E,CN⊥AB于N,如图3所示:
则∠BCN=30°,
∴BN=$\frac{1}{2}$BC=$\frac{1}{2}$,PE=CN=$\frac{\sqrt{3}}{2}$,
∵⊙P与⊙O相切,
∴OP=OB+PC=1+1-x=2-x,OE=OB+BN-EN=1+$\frac{1}{2}$-(1-x)=$\frac{1}{2}$+x,
由勾股定理得:OE2+PE2=OP2,
即($\frac{1}{2}$+x)2+($\frac{\sqrt{3}}{2}$)2=(2-x)2,
解得:x=$\frac{3}{5}$,
即BM为$\frac{3}{5}$时,⊙P与⊙O相切.
点评 本题是圆的综合题目,考查了平行四边形的性质、等边三角形的判定与性质、切线的判定、含30°角的直角三角形的性质、相切两圆的性质、勾股定理等知识;本题综合性强,有一定难度,特别是(3)②中,需要根据相切两圆的性质和勾股定理得出方程才能得出结果.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 如果a是整数,那么a是有理数 | |
| B. | 内错角相等 | |
| C. | 任何实数的绝对值都是正数 | |
| D. | 两边一角对应相等的两个三角形全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将两块直角三角尺的直角顶点C叠放在一起.
如图,将两块直角三角尺的直角顶点C叠放在一起.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知一次函数y1=-2x-3与y2=$\frac{1}{2}$x+2.
已知一次函数y1=-2x-3与y2=$\frac{1}{2}$x+2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com