
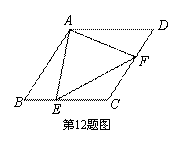
如图,在菱形ABCD中,∠B=60°,点E,F分别从点B,D同时以同样的速度沿边BC,DC向点C运动.给出以下四个结论:
① 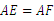 ;
;
② ∠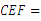 ∠
∠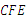 ;
;
③ 当点E,F分别为边BC,DC的中点时,△AEF是等边三角形;
④ 当点E,F分别为边BC,DC的中点时,△AEF的面积最大.
上述正确结论的序号有 .
科目:初中数学 来源: 题型:
古希腊数学家把数1,3,6,10,15,21,…叫做三角数,它有一定的规律性.若把第一个三角数记为a1,第二个三角数记为a2…,第n个三角数记为an,计算a1+a2,a2+a3,a3+a4,…由此推算a399+a400=
查看答案和解析>>
科目:初中数学 来源: 题型:
在某市组织的大型商业演出活动中,对团购买门票实行
优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6 000元购买的门票张数,现在只花费了4 800元.
(1)求每张门票的原定票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠措施,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
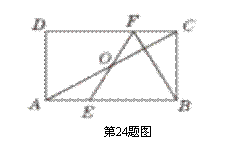
如图所示,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
(1)求证:OE=OF;
(2)若BC= ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读下面材料:
小凯遇到这样一个问题:如图1,在四边形ABCD中,对角线AC、BD相交于点O,
AC=4,BD=6,∠AOB=30°,求四边形ABCD的面积.
小凯发现,分别过点A、C作直线BD的垂线,垂足分别为点E、F,设AO为m,通过计算△ABD与△BCD的面积和使问题得到解决(如图2).
请回答:(1)△ABD的面积为 (用含m的式子表示).
(2)求四边形ABCD的面积.


|
|
 参考小凯思考问题的方法,解决问题:
参考小凯思考问题的方法,解决问题:
如图3,在四边形ABCD中,对角线AC、BD相交于
点O,
|
 (0°<
(0°< <90°),则四边形
<90°),则四边形 ABCD的面积为 (用含a、b、 的式子表示).
的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com