
如图所示,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
(1)求证:OE=OF;
(2)若BC= ,求AB的长.
,求AB的长.
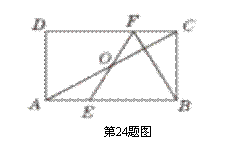
(1)证明:∵ 四边形ABCD是矩形,∴ AB∥CD.
∴ ∠OAE=∠OCF.
又∵ OA=OC, ∠AOE=∠COF,∴ △AEO≌△CFO(ASA).∴ OE=OF.
(2)解:连接BO.∵ BE=BF,∴ △BEF是等腰三角形.
又∵ OE=OF,∴ BO⊥EF,且∠EBO=∠FBO.∴ ∠BOF=90°.
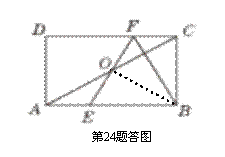
∵ 四边形ABCD是矩形,∴ ∠BCF=90°.
又∵ ∠BEF=2∠BAC,∠BEF=∠BAC+∠EOA,
∴ ∠BAC=∠EOA.∴ AE=OE.
∵ AE=CF,OE=OF,∴ OF=CF.
又∵ BF=BF,∴ Rt△BOF≌Rt△BCF(HL).
∴ ∠OBF=∠CBF.∴ ∠CBF=∠FBO=∠OBE.
∵ ∠ABC=90°,∴ ∠OBE=30°.∴ ∠BEO=60°.∴ ∠BAC=30°.
在Rt△BAC中,∵ BC=2 ,∴ AC=2BC=4
,∴ AC=2BC=4 .
.
AB=
点拨:证明线段相等的常用方法有以下几种:①等腰三角形中的等角对等边;②全等三角形中的对应边相等;③线段垂直平分线的性质;④角平分线的性质;⑤勾股定理;⑥借助第三条线段进行等量代换.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
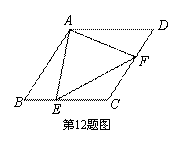
如图,在菱形ABCD中,∠B=60°,点E,F分别从点B,D同时以同样的速度沿边BC,DC向点C运动.给出以下四个结论:
① 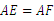 ;
;
② ∠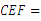 ∠
∠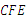 ;
;
③ 当点E,F分别为边BC,DC的中点时,△AEF是等边三角形;
④ 当点E,F分别为边BC,DC的中点时,△AEF的面积最大.
上述正确结论的序号有 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,AB=AC,AD是△ABC外角的平分线,已知∠BAC=∠ACD.
(1)求证:△ABC≌△CDA;
(2)若∠B=60°,求证:四边形ABCD是菱形.
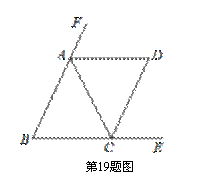
查看答案和解析>>
科目:初中数学 来源: 题型:
在面积为60的□ABCD中,过点A作AE⊥直线BC 于点E,作AF⊥直线CD于点F,若AB=10,BC=12,则CE+CF的值为…………………………………………( )
于点E,作AF⊥直线CD于点F,若AB=10,BC=12,则CE+CF的值为…………………………………………( )
A. 22+11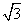 B. 22-11
B. 22-11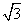
C. 22+11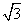 或22-11
或22-11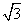 D. 22+11
D. 22+11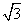 或2+
或2+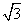
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com