
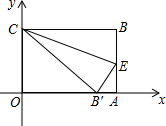
 如图,在直角坐标系中放入一个边长OC为9的矩形纸片ABCO.将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知tan∠OB′C=
如图,在直角坐标系中放入一个边长OC为9的矩形纸片ABCO.将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知tan∠OB′C=| 3 |
| 4 |
| 3 |
| 4 |
| CO |
| OB′ |
| 3 |
| 4 |
| 9 |
| OB′ |
| 3 |
| 4 |
| 92+122 |
| k |
| x |
| 60 |
| x |
| 60 |
| x |
| 20 |
| 3 |
| 20 |
| 3 |


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com