
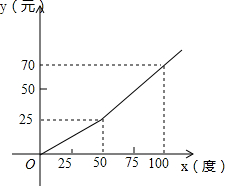
 为了缓解用电紧张矛盾,某电力公司特别制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.
为了缓解用电紧张矛盾,某电力公司特别制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.分析 (1)0≤x≤50时,函数为正比例函数,把(50,25)代入正比例函数解析式即可.x>50时,为一次函数解析式,把(50,25),(100,70)代入即可求得;
(2)把x=35代入y=$\frac{1}{2}$x,即可解答;
(3)把x=110代入y=0.9x-20,即可解答.
解答 解:(1)①当月用电量0≤x≤50时,y是x的正比例函数,
设y=k1x,
∵当x=50时,y=25,
∴25=50k1,
∴${k}_{1}=\frac{1}{2}$
∴y=$\frac{1}{2}$x.
②当月用电量x>50时,y是x的一次函数,
设y=k2x+b,∵当x=50时,y=25;当x=100时,y=70,
∴$\left\{\begin{array}{l}{50{k}_{2}+b=25}\\{100{k}_{2}+b=70}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{k}_{2}=0.9}\\{b=-20}\end{array}\right.$,
∴y=0.9x-20;
(2)把x=35代入y=$\frac{1}{2}$x,得:y=17.5,
答:当每月用电量为35度时,应缴电费17.5元;
(3)把x=110代入y=0.9x-20,得:y=99-20=79,
答:当每月用电量为110度时,应缴电费79元.
点评 本题考查了一次函数的应用,图中的函数为分段函数,注意自变量的取值范围相对应的函数值.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 每辆车的日租金x(元) | 200 | 220 | 240 | 270 | 300 | … |
| 日出租汽车数y(辆) | 100 | 96 | 92 | 86 | 80 | … |
| 出租汽车后的日收入(元) | 20000 | 21120 | 22080 | 23220 | 24000 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{10}$ | B. | $\sqrt{10}$ | C. | 2$\sqrt{5}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com