
| A. | 2$\sqrt{10}$ | B. | $\sqrt{10}$ | C. | 2$\sqrt{5}$ | D. | $\sqrt{5}$ |
分析 作点C关于AB的对称点M,连接DM与AB交于点E,连接AM、CM.此时ED+EC=DM最小,在RT△ADM中利用勾股定理即可求出最小值.
解答 解:如图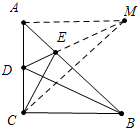 作点C关于AB的对称点M,连接DM与AB交于点E,连接AM、CM.此时ED+EC最小,
作点C关于AB的对称点M,连接DM与AB交于点E,连接AM、CM.此时ED+EC最小,
∵EC=EM,AC=AM=4,
∴ED+EC=EM+ED=DM,
在RT△ADM中,∵AD=DC=2,AM=4,
∴DM=$\sqrt{A{M}^{2}+A{D}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∴ED+EC的最小值=2$\sqrt{5}$.
故选C.
点评 本题考查轴对称-最短问题、勾股定理等知识,解决问题的关键是利用两点之间线段最短找到点E的位置,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
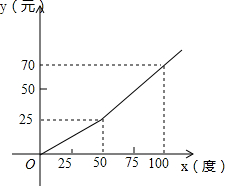 为了缓解用电紧张矛盾,某电力公司特别制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.
为了缓解用电紧张矛盾,某电力公司特别制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 参加班级 | A | B | C | D |
| 得分情况 | 14 | 18 | 10 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
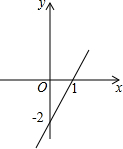 如图,已知一次函数y=kx+b(k、b为常数,k≠0)的图象,当y>-2时,x的取值范围为( )
如图,已知一次函数y=kx+b(k、b为常数,k≠0)的图象,当y>-2时,x的取值范围为( )| A. | x<1 | B. | x>1 | C. | x<0 | D. | x>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在边长为12$\sqrt{2}$的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG交EG于H,交AD于F点,连接CE,BH.若BH=16,则FG=10$\sqrt{2}$.
如图,在边长为12$\sqrt{2}$的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG交EG于H,交AD于F点,连接CE,BH.若BH=16,则FG=10$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com