
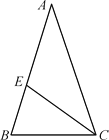
【题目】如图,△ABC中,AB=AC,∠A=36,CE平分∠ACB交AB于点E.
(1)试说明点E为线段AB的黄金分割点;
(2)若AB=4,求BC的长.
【答案】(1)证明见解析;(2)![]()
【解析】
试题(1)根据等腰三角形两底角相等求出∠ACB=72°,再根据角平分线的定义求出∠BCE=36°,从而得到∠BCE=∠A,然后判定△ABC和△CBE相似,根据相似三角形对应边成比例列出比例式整理,并根据黄金分割点的定义即可得证;
(2)根据等角对等边的性质可得AE=CE=BC,再根据黄金分割求解即可.
试题解析:(1)证明:∵AB=AC,∠A=36°,
∴∠ACB=![]() (180°-36°)=72°,
(180°-36°)=72°,
∵CE平分∠ACB,
∴∠BCE=![]() ∠ACB=
∠ACB=![]() ×72°=36°,
×72°=36°,
∴∠BCE=∠A=36°,
∴AE=BC,
又∵∠B=∠B,
∴△ABC∽△CBE,
∴![]() ,
,
∴BC2=ABBE,
即AE2=ABBE,
∴E为线段AB的黄金分割点;
(2)∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∴∠BEC=180°-72°-36°=72°,
∴BC=CE,
由(1)已证AE=CE,
∴AE=CE=BC,
∴BC=![]() AB=
AB=![]() ×4=2
×4=2![]() -2.
-2.


科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 为原点,点
为原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .抛物线
.抛物线![]() 经过点
经过点![]() ,
,![]() ,与
,与![]() 交于点
交于点![]() .
.
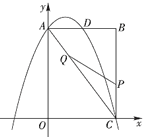
(1)求抛物线的函数解析式;
(2)![]() 为线段
为线段![]() 上一个动点(不与点
上一个动点(不与点![]() 重合),
重合),![]() 为线段
为线段![]() 上一个动点,
上一个动点,![]() ,连接
,连接![]() ,设
,设![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值及此时点
的最大值及此时点![]() 的坐标;
的坐标;
(3)在(2)的条件下,![]() 为抛物线
为抛物线![]() 的对称轴
的对称轴![]() 上一点,请求出使
上一点,请求出使![]() 为锐角三角形时,点
为锐角三角形时,点![]() 的纵坐标
的纵坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明解方程![]() =3出现了错误,解答过程如下:
=3出现了错误,解答过程如下:
方程两边都乘以(x-2),得1-(1-x)=3(第一步)
去括号,得1-1+x=3(第二步)
移项,合并同类项,得x=3(第三步)
检验,当x=3时x-2≠0(第四步)
所以x=3是原方程的解.(第五步)
(1)小明解答过程是从第____步开始出错的,原方程化为第一步的根据是_____.
(2)请写出此题正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠C=90°,AC=8cm,BC=6cm.动点P在线段AC上以5cm/s的速度从点A运动到点C.过点P作PD⊥AB于点D,将△APD绕PD的中点旋转180°得到△A'DP.设点P的运动时间为x(s).
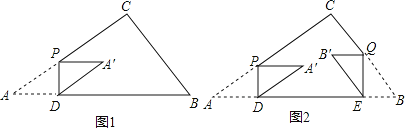
(1)求点A'落在边BC上时x的值.
(2)设△A'DP和△ABC重叠部分图形周长为y(cm),求y与x之间的函数关系式.
(3)如图②,另有一动点Q与点P同时出发,在线段BC上以5cm/s的速度从点B运动到点C.过点Q作QE⊥AB于点E,将△BQE绕QE的中点旋转180°得到△B'EQ.连结A′B′.当直线A'B'与△ABC的边垂直或平行时,直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与x轴最多有一个交点.现有以下四个结论:①
与x轴最多有一个交点.现有以下四个结论:①![]() ;②该抛物线的对称轴在y轴的左侧;③关于x的方程
;②该抛物线的对称轴在y轴的左侧;③关于x的方程![]() 有实数根;④
有实数根;④![]() .其中正确结论的个数为( )
.其中正确结论的个数为( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有![]() 、
、![]() 两地,甲乙两人同时出发,甲骑自行车从
两地,甲乙两人同时出发,甲骑自行车从![]() 地到
地到![]() 地,乙骑自行车从
地,乙骑自行车从![]() 地到
地到![]() 地,到达
地,到达![]() 地后立即按原路返回
地后立即按原路返回![]() 地.如图是甲、乙两人离
地.如图是甲、乙两人离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数图象,下列说法中①
之间的函数图象,下列说法中①![]() 、
、![]() 两地相距30千米;②甲的速度为15千米/时;③点
两地相距30千米;②甲的速度为15千米/时;③点![]() 的坐标为(
的坐标为(![]() ,20);④当甲、乙两人相距10千米时,他们的行驶时间是
,20);④当甲、乙两人相距10千米时,他们的行驶时间是![]() 小时或
小时或![]() 小时. 正确的个数为( )
小时. 正确的个数为( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
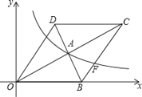
【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数y=![]() (x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
(1)求反比例函数的表达式;
(2)求BC所在直线的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com