练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．△ABC的三边a、b、c满足|a+b-50|+$\sqrt{a-b-32}$+（c-40）2=0．试判断△ABC的形状是直角三角形．

    分析 先利用非负数的性质，分别求出a、b、c的值，然后利用勾股定理的逆定理证明△ABC是直角三角形．

    解答 解：∵|a+b-50|+$\sqrt{a-b-32}$+（c-40）2=0，
    ∴$\left\{\begin{array}{l}{a+b-50=0}\\{a-b-32=0}\\{c-40=0}\end{array}\right.$，
    解得$\left\{\begin{array}{l}{a=41}\\{b=9}\\{c=40}\end{array}\right.$，
    ∵92+402=412，
    ∴△ABC是直角三角形．
    故答案为直角三角形．

    点评 此题主要考查了勾股定理的逆定理以及绝对值、偶次方和算术平方根的性质，得出a、b、c的值是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    11．若分式$\frac{2x-y}{y}$中的x，y的值变为原来的2倍，则此分式的值（　　）
    A．不变B．发生变化C．是原来的2倍D．是原来的$\frac{1}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

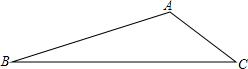    12．△ABC是武汉市在拆除违章建筑后的一块三角形空地，已知∠A=150°，AB=30m，AC=20m，如果要在这块空地上种草皮，按每平方米a元计算，则需要资金多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．计算：$|{\sqrt{2}-\sqrt{3}}|+6\sqrt{2}+2\sqrt{3}-5\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，直线AB，CD被直线GH所截，且∠AEG=∠CFG，EM，FN分别平分∠AEG和∠CFG．试说明EM∥FN．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．已知$\left\{\begin{array}{l}{2x-y=1}\\{x+4y=3}\end{array}\right.$，则x+y=$\frac{4}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．如图，△ABC中，AD是∠BAC的角平分线，AB=4，AC=3，则△ABD与△ADC的面积比是4：3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图，AB⊥AC，垂足为A，CD⊥AC，垂足为C，DE⊥BC，且AB=CE，若BC=5cm，则DE的长为5cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

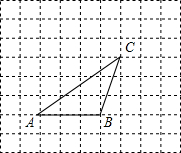    11．在正方形网格中，△ABC的位置如图所示，则sin∠BAC的值为（　　）
    A．$\frac{3}{5}$B．$\frac{3}{4}$C．$\frac{4}{5}$D．$\frac{4}{3}$

    查看答案和解析>>

    同步练习册答案