
【题目】如图1,在正方形![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
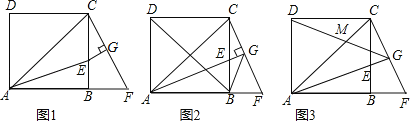
(1)求证:![]() ;
;
(2)如图2,连接![]() 、
、![]() ,求证:
,求证:![]() 平分
平分![]() ;
;
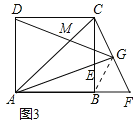
(3)如图3,连接![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)由正方形性质得出![]() ,
,![]() ,根据直角三角形两锐角互余的关系可得
,根据直角三角形两锐角互余的关系可得![]() ,利用
,利用![]() 可证得
可证得![]() ,即可得出结论;(2)由正方形性质与角平分线的定义得出
,即可得出结论;(2)由正方形性质与角平分线的定义得出![]() ,利用
,利用![]() 可证得
可证得![]() 得出
得出![]() ,由直角三角形斜边中线的性质得出
,由直角三角形斜边中线的性质得出![]() ,根据角的和差关系可得
,根据角的和差关系可得![]() ,即可得出结论;(3)连接
,即可得出结论;(3)连接![]() ,由正方形的性质得出
,由正方形的性质得出![]() ,
,![]() ,
,![]() ,推出
,推出![]() ,根据角的和差关系可得
,根据角的和差关系可得![]() ,利用
,利用![]() 可证得
可证得![]() ,得出
,得出![]() ,推出
,推出![]() ,即可证得△DCM∽△ACE,即可得出结果.
,即可证得△DCM∽△ACE,即可得出结果.
(1)∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,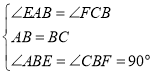 ,
,
∴![]() ,
,
∴![]() .
.
(2)证明:∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,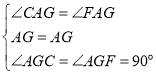 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
∴![]()
![]() ,
,
∴![]() ,
,
∴![]() 平分
平分![]() .
.
(3)解:连接![]() ,如图3所示:
,如图3所示:
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]()
![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() =22.5°,
=22.5°,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中,放入2个白球和1个红球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出1个球,记录下颜色后放回袋中,再次搅匀后从中任意摸出1个球,请通过列表或画树状图求2次摸出的球都是白球的概率;
(2)搅匀后从中任意一次摸出2个球,则摸出的2个球都是白球的概率为 ;
(3)现有一个可以自由转动的转盘,转盘被等分成60个相等的扇形,这些扇形除颜色外完全相同,其中40个扇形涂上白色,20个扇形涂上红色,转动转盘2次,指针2次都指向白色区域的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数是( )
A. 70° B. 35° C. 40° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5条.设每条裤子的售价为![]() 元(
元(![]() 为正整数),每月的销售量为
为正整数),每月的销售量为![]() 条.
条.
(1)直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)设该网店每月获得的利润为![]() 元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆,售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是20元.调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元,每减少1盆,盆景的平均每盆利润增加2元;
②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加![]() 盆,第二期盆景与花卉售完后的利润分别为
盆,第二期盆景与花卉售完后的利润分别为![]() ,
,![]() (单位:元)
(单位:元)
(1)用含![]() 的代数式分别表示
的代数式分别表示![]() ,
,![]() .
.
(2)当![]() 取何值时,第二期培植的盆录与花卉售完后获得的总利润
取何值时,第二期培植的盆录与花卉售完后获得的总利润![]() 最大,最大总利润是多少?
最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“文化宜昌全民阅读”活动中,某中学社团“精一读书社”对全校学生的人数及纸质图书阅读量(单位:本)进行了调查,2012年全校有1000名学生,2013年全校学生人数比2012年增加10%,2014年全校学生人数比2013年增加100人.
(1)求2014年全校学生人数;
(2)2013年全校学生人均阅读量比2012年多1本,阅读总量比2012年增加1700本(注:阅读总量=人均阅读量×人数)
①求2012年全校学生人均阅读量;
②2012年读书社人均阅读量是全校学生人均阅读量的2.5倍,如果2012年、2014年这两年读书社人均阅读量都比前一年增长一个相同的百分数a,2014年全校学生人均阅读量比2012年增加的百分数也是a,那么2014年读书社全部80名成员的阅读总量将达到全校学生阅读总量的25%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系![]() 中,点
中,点![]() ,函数
,函数![]() (
(![]() )的图象经过平行四边形
)的图象经过平行四边形![]() 的顶点
的顶点![]() 和边
和边![]() 的中点
的中点![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 的面积等于6.求
的面积等于6.求![]() 的值;
的值;
(3)若![]() 为函数
为函数![]() (
(![]() )的图象上一个动点,过点
)的图象上一个动点,过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,直线
,直线![]() 与
与![]() 轴上方的平行四边形
轴上方的平行四边形![]() 的一边交于点
的一边交于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后来经过市场调查发现,单价每降低 10 元,则平均每周的销售量可增加 40 千克,若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元,请回答:
(1)每千克茶叶应降价多少元?
(2)在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的 几折出售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com