
【题目】如图,平面直角坐标系![]() 中,点
中,点![]() ,函数
,函数![]() (
(![]() )的图象经过平行四边形
)的图象经过平行四边形![]() 的顶点
的顶点![]() 和边
和边![]() 的中点
的中点![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 的面积等于6.求
的面积等于6.求![]() 的值;
的值;
(3)若![]() 为函数
为函数![]() (
(![]() )的图象上一个动点,过点
)的图象上一个动点,过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,直线
,直线![]() 与
与![]() 轴上方的平行四边形
轴上方的平行四边形![]() 的一边交于点
的一边交于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)根据平行四边形的性质确定出B的坐标从而确定出D的坐标,而点A,D在反比例函数图象上,建立方程求出m,
(2)根据三角形OAD的面积是平行四边形OABC面积的一半,确定出n即可;
(3)根据题意可得情况讨论①点![]() 在
在![]() 上,②当点
上,②当点![]() 在
在![]() 上,求出两种情况下点M,N,P的坐标,即可求出MP,NP的长度结合
上,求出两种情况下点M,N,P的坐标,即可求出MP,NP的长度结合![]() ,求解即可.
,求解即可.
解:(1)∵点![]() ,平行四边形
,平行四边形![]() 的顶点
的顶点![]()
∴![]()
∴![]()
∵函数![]() (
(![]() )的图象经过平行四边形
)的图象经过平行四边形![]() 的顶点
的顶点![]() 和边
和边![]() 的中点
的中点![]()
∴![]() ,
,![]()
∴![]()
(2)∵点![]() 是平行四边形
是平行四边形![]() 中点
中点
∴![]()
∵![]()
∴![]()
由(1)知,![]()
∴![]()
(3)①如图1,点![]() 在
在![]() 上,
上,
由(1)知,![]()
∴![]()
即![]()
直线![]() 的解析式为
的解析式为![]() ,
,
设点![]() 的横坐标为
的横坐标为![]()
∴![]()
∵过点![]() 作直线
作直线![]() 轴于点
轴于点![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
∵![]()
∴![]()
∴![]() 或
或![]() (舍)
(舍)
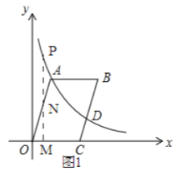
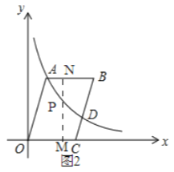
②如图2,
当点![]() 在
在![]() 上时,
上时,
由(1)知,![]()
∴![]()
由题意知,![]() ,
,![]() ,
,![]()
∵![]()
∴![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
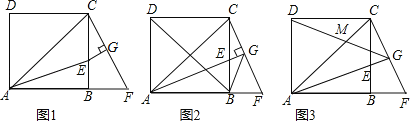
(1)求证:![]() ;
;
(2)如图2,连接![]() 、
、![]() ,求证:
,求证:![]() 平分
平分![]() ;
;
(3)如图3,连接![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家将于5月1日进行自驾游,由于交通便利,准备将行程分为上午和下午.上午的备选地点为:A—鼋头渚、B—常州淹城春秋乐园、C—苏州乐园,下午的备选地点为:D—常州恐龙园、E—无锡动物园.
(1)请用画树状图或列表的方法分析并写出小明家所有可能的游玩方式(用字母表示即可);
(2)求小明家恰好在同一城市游玩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形![]() 的边长为2,以点
的边长为2,以点![]() 为圆心,1为半径作圆,
为圆心,1为半径作圆,![]() 是圆
是圆![]() 上的任意一点,将点
上的任意一点,将点![]() 绕点
绕点![]() 按逆时针方向转转
按逆时针方向转转![]() ,得到点
,得到点![]() ,连接
,连接![]() ,则
,则![]() 的最大值是__________.
的最大值是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
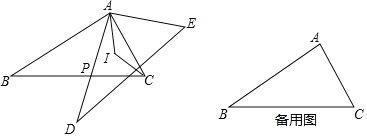
【题目】如图,△ABC和△ADE中,AB=AD=6,BC=DE,∠B=∠D=30°,边AD与边BC交于点P(不与点B,C重合),点B,E在AD异侧,I为△APC的内心.
(1)求证:∠BAD=∠CAE;
(2)设AP=x,请用含x的式子表示PD,并求PD的最大值;
(3)当AB⊥AC时,∠AIC的取值范围为m°<∠AIC<n°,分别直接写出m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)每件童装降价多少元时,平均每天赢利1200元.
(2)每件童装售价为多少元时,平均每天赢利最大,并求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
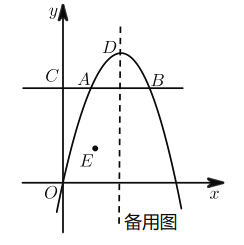
【题目】如图,在平面直角坐标系中,点A在抛物线y=- x2 + 4x上,且横坐标为1,点B与点A关于抛物线的对称轴对称,直线AB与y轴交于点C,点D为抛物线的顶点,点E的坐标为(1,1).
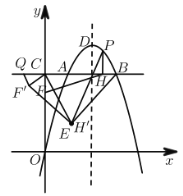
(1)求线段AB的长.
(2)点P为线段AB.上方抛物线上的任意一点,过点P作AB的垂线交AB于点H,点F为y轴上一点,当![]() PBE的面积最大时,求PH + HF +
PBE的面积最大时,求PH + HF + ![]() FO的最小值.
FO的最小值.
(3)在(2)中,PH+HF+![]() 方FO取得最小值时,将
方FO取得最小值时,将![]() CFH绕点C顺时针旋转60°后得到
CFH绕点C顺时针旋转60°后得到![]() CF'H',过点F'作CF'的垂线与直线AB交于点Q,点R为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S,使以点D,Q,R,S为顶点的四边形为菱形,若存在,请直接写出点S的坐标,若不存在,请说明理由.
CF'H',过点F'作CF'的垂线与直线AB交于点Q,点R为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S,使以点D,Q,R,S为顶点的四边形为菱形,若存在,请直接写出点S的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】石狮泰禾某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售______ 件,每件盈利______ 元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com