Question

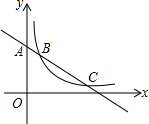
15．如图，直线y=-$\frac{\sqrt{3}}{3}$x+b与y轴交于点A，与双曲线y=$\frac{k}{x}$在第一象限交于B、C两点，且AB•AC=4，则k=（　　）

• A． $\frac{\sqrt{3}}{2}$
• B． $\frac{\sqrt{3}}{3}$
• C． $\sqrt{3}$
• D． 2$\sqrt{3}$

Answer 1

分析 设直线y=-$\frac{\sqrt{3}}{3}$x+b与x轴交于点D，作BE⊥y轴于E，CF⊥y轴于F．先求出直线与x轴和y轴的两交点D与A的坐标，根据OA与OD的长度求出比值即可得到角ADO的正切值，利用特殊角的三角函数值求出角ADO的度数，联立直线与双曲线方程，消去y后得到关于x的一元二次方程，利用韦达定理表示出EB与FC的积，然后在直角三角形AEB中利用cos∠ABE表示出EB与AB的关系，同理在直角三角形AFC中，利用cos∠ACF表示出FC与AC的关系，根据AB•AC=4列出关于k的方程，求出方程的解即可得到k的值．

解答 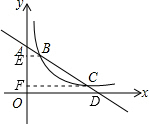解：设直线y=-$\frac{\sqrt{3}}{3}$x+b与x轴交于点D，作BE⊥y轴于E，CF⊥y轴于F．
∵y=-$\frac{\sqrt{3}}{3}$x+b，
∴当y=0时，x=$\sqrt{3}$b，即点D的坐标为（$\sqrt{3}$b，0），
当x=0时，y=b，即A点坐标为（0，b），
∴OA=b，OD=$\sqrt{3}$b．
∵在Rt△AOD中，tan∠ADO=$\frac{OA}{OD}$=$\frac{b}{\sqrt{3}b}$=$\frac{\sqrt{3}}{3}$，
∴∠ADO=30°．
∵直线y=-$\frac{\sqrt{3}}{3}$x+b与双曲线y=$\frac{k}{x}$在第一象限交于点B、C两点，
∴-$\frac{\sqrt{3}}{3}$x+b=$\frac{k}{x}$，
整理得，-$\frac{\sqrt{3}}{3}$x²+bx-k=0，
由韦达定理得：x₁x₂=$\frac{-k}{-\frac{\sqrt{3}}{3}}$=$\sqrt{3}$k，即EB•FC=$\sqrt{3}$k，
∵$\frac{EB}{AB}$=cos30°=$\frac{\sqrt{3}}{2}$，
∴AB=$\frac{2\sqrt{3}}{3}$EB，
同理可得：AC=$\frac{2\sqrt{3}}{3}$FC，
∴AB•AC=（$\frac{2\sqrt{3}}{3}$EB）（$\frac{2\sqrt{3}}{3}$FC）=$\frac{4}{3}$EB•FC=$\frac{4}{3}$×$\sqrt{3}$k=4，
解得：k=$\sqrt{3}$．
故选C．

点评 本题考查的是反比例函数与一次函数的交点问题及根与系数的关系，解答此题的关键根据题意作出辅助线，根据锐角三角函数的定义沟通各线段之间的关系．