
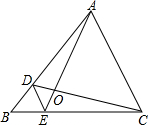
 如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,求S△DOE:S△AOC的值.
如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,求S△DOE:S△AOC的值. 分析 由已知得出BE:BC=1:4;证明△DOE∽△AOC,得到$\frac{DE}{AC}=\frac{1}{4}$,由相似三角形的性质即可解决问题.
解答 解:∵S△BDE:S△CDE=1:3,
∴BE:EC=1:3;
∴BE:BC=1:4;
∵DE∥AC,
∴△DOE∽△AOC,
∴$\frac{DE}{AC}=\frac{BE}{BC}$=$\frac{1}{4}$,
∴S△DOE:S△AOC=($\frac{1}{4}$)=$\frac{1}{16}$.
点评 本题主要考查了相似三角形的判定及其性质的应用问题;熟练掌握相似三角形的判定与性质,证出BE:BC=1:4是解决问题的关键解题的关键.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运输工具 | 途中平均速度 (千米/时) | 运费 (元/千米) | 装卸费用 (元) |
| 火车 | 100 | 15 | 2000 |
| 汽车 | 80 | 20 | 900 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售单价(元) | x(x>30) |
| 销售量y(件) | -10x+800 |
| 销售玩具获得利润w(元) | -10x2+1000x-16000 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com