练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．（1-$\frac{1}{{2}^{2}}$）（1-$\frac{1}{{3}^{2}}$）（1-$\frac{1}{{4}^{2}}$）…（1-$\frac{1}{100{4}^{2}}$）

    分析 原式利用平方差公式化简，结合后相乘即可得到结果．

    解答 解：原式=（1+$\frac{1}{2}$）（1+$\frac{1}{3}$）…（1+$\frac{1}{1004}$）（1-$\frac{1}{2}$）（1-$\frac{1}{3}$）…（1-$\frac{1}{1004}$）=$\frac{3}{2}$×$\frac{4}{3}$×$\frac{5}{4}$×…×$\frac{1005}{1004}$×$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$×…×$\frac{1003}{1004}$=$\frac{1005}{2}$×$\frac{1}{1004}$=$\frac{1005}{2008}$．

    点评 此题考查了平方差公式，熟练掌握平方差公式是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    2．分解因式：
    （1）m4-16n4；
    （2）x2（x-y）+（y-x）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．（1）解分式方程：$\frac{x}{x-2}$-1=$\frac{6}{x+2}$；
    （2）化简求值：$\frac{a-b}{a}$÷（a-$\frac{2ab-{b}^{2}}{a}$），其中a=$\sqrt{2}$，b=$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．一个多项式加上3+x-2x2，得到x2-1，则这个多项式是3x2-x-4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

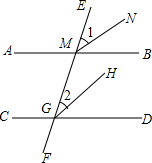    7．如图，直线AB∥CD，EF分别交AB、CD于点M、G，MN平分∠EMB，GH平分∠MGD，求证：MN∥GH．
    证明：∵AB∥CD已知
    ∴∠EMB=∠EGD两直线平行，同位角相等
    ∵MN平分∠EMB，GH平分∠MGD（已知）
    ∴∠1=$\frac{1}{2}$∠EMB，∠2=$\frac{1}{2}$∠MGD角平分线的定义
    ∴∠1=∠2
    ∴MN∥GH同位角相等，两直线平行．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

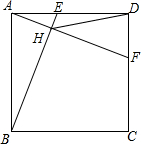    17．如图，E，F是正方形ABCD边AD，CD上两个动点，且AE=DF，BE交AF于H，AB=2，连接DH．
    （1）求证：AF⊥BE；
    （2）求线段DH的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．分解因式：
    （1）（2x+1）2-x2；
    （2）8a-4a2-4；
    （3）x4-16；                   
    （4）1-a2+2ab-b2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．计算：
    （1）-12002-$\frac{1}{7}×$[2-（-3）2]；
    （2）（-2）2+（-2）÷（-$\frac{2}{3}$）+|-$\frac{1}{16}$|×（-24）；
    （3）$\frac{y}{5}$-$\frac{y-1}{2}$=1-$\frac{y+2}{5}$；           
    （4）6-3（x+$\frac{2}{3}$）=$\frac{2}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，你能否判断∠1+∠2与∠B+∠C的大小关系？并说明理由．

    查看答案和解析>>

    同步练习册答案