
����Ŀ����ͼ1����֪��M��x�ύ��A��B���㣬��y�ύ��C��D���㣬A��B����ĺ�����ֱ�Ϊ��1��7����AB�����ľ�MNΪ3��
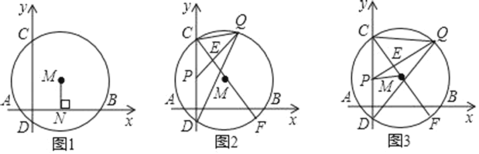
��1�����M�İ뾶��
��2����ͼ2��P����CD�ϣ���CP��2��Q�ǻ�BC��һ���㣬PQ��ֱ��CF�ڵ�E������CPQ����CQDʱ��
���ж��߶�PQ��ֱ��CF��λ�ù�ϵ����˵�����ɣ�
����CQ�ij���
��3����ͼ3����P������CD��һ���㣬Q�ǻ�BC��һ���㣬PQ��ֱ��CF�ڵ�E������CPQ���CQD����ʱ�����PEM��������ֵ��
���𰸡���1��5����2����PQ��CF�������������4����3����PEM��������ֵΪ3
��������
��1������MB����������ó�AB=8���ٽ�ϴ��������ɵ�BN=4������һ�����ù��ɶ���������⼴�ɣ�
��2��������DF����Բ�ܽǶ����ó���CDF=90�����ɴ˽�һ��֤����CEP��90�����ɣ�����MN��AB��N��MG��CD��G���ӳ�QP����M��H���Ӷ�ͨ�������ɵ�AN=4��MN=3,MG=ON=3�����ߵó�MN=MG����һ��֤��CD=AB=8��Ȼ�����ù��ɶ������DF=6������֤����CPE���CFD���ƣ������������������ʵó�CE��PE�ij����Ӷ����EF������ڴ˻����Ͻ�һ��������⼴�ɣ�
��3����֤����DCF=��CPQ���ó�CE=PE������EK��CP��K��PT��CM��T������DF����CK��PK��![]() ���ݴ���EK��3x����CK��4x��CE��PE��5x��PC��8x������֤����CPT~��CFD�������������������ʵó�PT��
���ݴ���EK��3x����CK��4x��CE��PE��5x��PC��8x������֤����CPT~��CFD�������������������ʵó�PT��![]() ��CT��
��CT��![]() �������������������ʽ�õ���PEM�����
�������������������ʽ�õ���PEM�����![]() ���ɴ����ö��κ��������ʽ�һ����⼴��.
���ɴ����ö��κ��������ʽ�һ����⼴��.
��1������MB����ͼ1��ʾ��

��A��B����ĺ�����ֱ�Ϊ![]() ��7��
��7��
��AB��8��
��MN��AB��
��BN��4��
��Rt��BMN�У��ɹ��ɶ����ã�
![]() ��
��
���M�İ뾶Ϊ5��
��2����PQ��CF���������£�
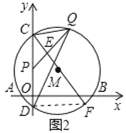
����DF����ͼ2��ʾ��
��CF�ǡ�M��ֱ����
���CDF��90�㣬
���CFD+��DCF��90�㣬
�ߡ�CQD����CFD��
���CQD+��DCF��90�㣬
�ߡ�CPQ����CQD��
���CPQ+��DCF��90�㣬
���CEP��90�㣬
��PQ��CF��
����MN��AB��N��MG��CD��G���ӳ�QP����M��H����ͼ3��ʾ��
��AN��4��MN��3��MG��ON��3��
��MN��MG��
��CD��AB��8��
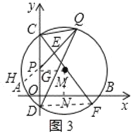
��Rt��CDF��CF��2BM��10��![]() ��
��
�ɢٵã�PQ��CF��
���CEP����CDF��90�㣬EH��EQ��
�ߡ�PCE����FCD��
���CPE~��CFD��
��![]() ��
��
��![]() ��
��
��ã�CE��![]() ��PE��
��PE��![]() ��
��
��EF��CFCE��![]() ��
��
��EQ��EH��CE��EF����![]() ��
��
��Rt��CPE�У��ɹ��ɶ����ã�![]() ��
��
��3����CF�ǡ�M��ֱ����
���CDF��90�㣬
���F+��DCF��90�㣬
�ߡ�CQD����F��
���CQD+��DCF��90�㣬
�ߡ�CPQ+��CQD��90�㣬
���DCF����CPQ��
��CE��PE��
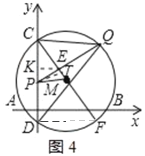
��EK��CP��K��PT��CM��T��������DF����ͼ4��ʾ��
��CK��PK��![]() ��
��
��EK��3x����CK��4x��CE��PE��5x��PC��8x��
�ߡ�PCT=��DCF����CTP=��CDF=90�㣬
���CPT~��CFD��
��![]() ��
��
��PT��![]() ��CT��
��CT��![]() ��
��
���PEM�����![]() ��
��
��![]() ��
��
��S�����ֵ���ҵ�![]() ʱ��S�����ֵΪ3��
ʱ��S�����ֵΪ3��
����PEM��������ֵΪ3��


 �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
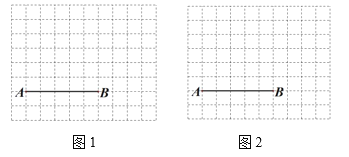
����Ŀ��ͼ1��ͼ2�ֱ���![]() ������������ÿ��С�����εı߳���Ϊ1��
������������ÿ��С�����εı߳���Ϊ1��![]() ��
��![]() ������С�����εĶ����ϣ�����ͼ1��ͼ2�и�ȡһ��
������С�����εĶ����ϣ�����ͼ1��ͼ2�и�ȡһ��![]() ����
����![]() ������С�����εĶ����ϣ���ʹ��
������С�����εĶ����ϣ���ʹ��![]() ��
��![]() ��
��![]() Ϊ����������ηֱ���������Ҫ��
Ϊ����������ηֱ���������Ҫ��
��1����ͼ1�л�һ��![]() ��ʹ
��ʹ![]() ����
����![]() Ϊб�ߵ�ֱ�������Σ���
Ϊб�ߵ�ֱ�������Σ���![]() ��
��
��2����ͼ2�л�һ��![]() ��ʹ
��ʹ![]() Ϊ���������Σ���
Ϊ���������Σ���![]() ��ֱ��д��
��ֱ��д��![]() �ij��ȣ�
�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������P��BA���ӳ����ϣ�PA��AO��PD���O�����ڵ�D��BC��AB��PD���ӳ����ڵ�C������O�İ뾶Ϊ1����BC�ij��ǣ�������
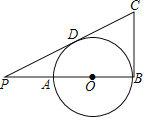
A.1.5B.2C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ����һ���㣨�����
����һ���㣨�����![]() �غϣ�����
�غϣ�����![]() Ϊ�߳���������
Ϊ�߳���������![]() ������
������![]() ����
����![]() ����������ֵ����________��
����������ֵ����________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ž���ֽ���Բ��ֽ�尴��ͼ��ʽ�ֱ����ͬ����������ͼ��AC=3��BC=4��AB=5���ֱ������߳������������) ��ͼ1�б�HI��LM�͵�K��J��ǡ���ھ���ֽ��ı��ϣ�ͼ2�е�Բ��O��AB�е㴦����H��I����Բ�ϣ�����κ�Բ��ֽ���������ǣ� ��
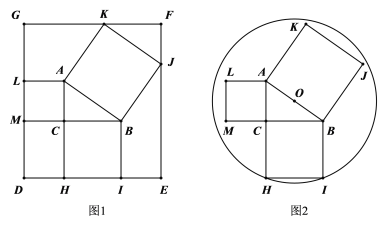
A.400:127��B.484:145��C.440:137��D.88:25��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
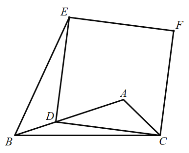
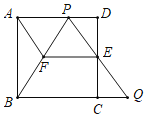
����Ŀ����ͼ���ڱ߳�Ϊl��������ABCD�У�E�DZ�CD���е㣬��P�DZ�AD��һ�㣨���A��D���غϣ�������PE��BC���ӳ��߽��ڵ�Q��
��1����֤��![]() ��
��
��2������E��![]() ��PB�ڵ�F������AF����
��PB�ڵ�F������AF����![]() ʱ������֤���ı���AFEP��ƽ���ı��Σ�
ʱ������֤���ı���AFEP��ƽ���ı��Σ�
�����ж��ı���AFEP�Ƿ�Ϊ���Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ƽ��ֱ������ϵ�У���![]() Ϊ����ԭ�㣬������
Ϊ����ԭ�㣬������![]() ��
��![]() ����
����![]() ��
��![]() ���㣨��
���㣨��![]() �ڵ�
�ڵ�![]() ���ұߣ���
���ұߣ���![]() ���ڵ�
���ڵ�![]() ��
��![]() ��
��
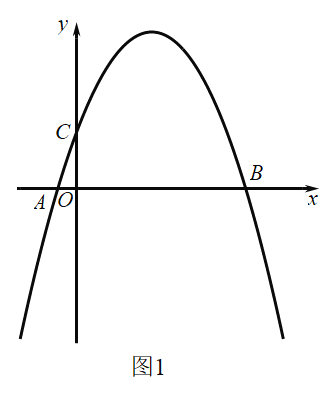
��1����ͼ1���������ߵĽ���ʽ��
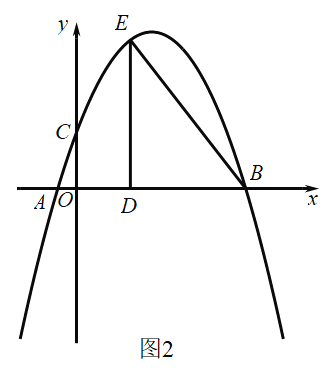
��2����ͼ2����![]() �ǵ�һ�����������ϵĵ㣬����
�ǵ�һ�����������ϵĵ㣬����![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ����
����![]() �������
�������
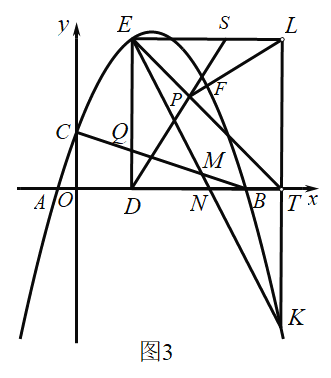
��3����ͼ3���ڣ�2���������£�����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ǵ��������������ϵĵ㣬����
�ǵ��������������ϵĵ㣬����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ���ڵ�
���ڵ�![]() ��
��![]() ������
������![]() ��ֱ��
��ֱ��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() �ᣬ��ֱ��
�ᣬ��ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() �������߶Գ����Ҳ��һ�����������ϵĵ㣬����
�������߶Գ����Ҳ��һ�����������ϵĵ㣬����![]() ��
��![]() ��
��![]() ���ӳ��߽�
���ӳ��߽�![]() �ڵ�
�ڵ�![]() ������
������![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() ��
��![]() �����
�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶�� ![]() ��ѧ��������������ǰ�����ȡ����ѧ�������������ԣ����ݲ��Գɼ�����������������������ͳ��ͼ������������Ϣ������������⣺
��ѧ��������������ǰ�����ȡ����ѧ�������������ԣ����ݲ��Գɼ�����������������������ͳ��ͼ������������Ϣ������������⣺
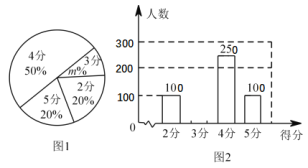
��1�����βμ��������Ե�ѧ������Ϊ ��ͼ ![]() ��
�� ![]() ��ֵΪ ��
��ֵΪ ��
��2���ε����ȡ���������ݵ�ƽ��������������λ����
��3�������������ݣ����Ƹ�У���꼶���������е� ![]() �ֵ�ѧ��Լ�ж�����?
�ֵ�ѧ��Լ�ж�����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
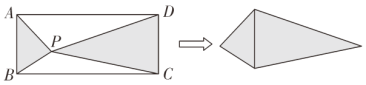
����Ŀ����ͼ���ھ���![]() �У�
��![]() ��
��![]() ��P�Ǿ���
��P�Ǿ���![]() ��һ�㣬��
��һ�㣬��![]() ��
��![]() ��
��![]() ��
��![]() ��������μ�����Ȼ���������Ӱ������ƴ��һ���ı��Σ�������ı��ε����Ϊ_________������ı����ܳ�����СֵΪ________.
��������μ�����Ȼ���������Ӱ������ƴ��һ���ı��Σ�������ı��ε����Ϊ_________������ı����ܳ�����СֵΪ________.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com