
 如图,△ABC中,AB=AC,△ABC的周长是32,且cosB=
如图,△ABC中,AB=AC,△ABC的周长是32,且cosB=| 3 |
| 5 |
| 3 |
| 5 |
| BD |
| AB |
| 3 |
| 5 |
| BE |
| BC |
| 3 |
| 5 |
| AE |
| AC |
| ||
| 10 |
| 14 |
| 50 |
| 7 |
| 25 |
| 24 |
| 25 |
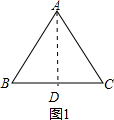 解:(1)如图1,作AD⊥BC于D,
解:(1)如图1,作AD⊥BC于D,| 3 |
| 5 |
| BD |
| AB |
| 3 |
| 5 |
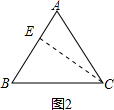 作CE⊥AB于E,
作CE⊥AB于E,| 3 |
| 5 |
| BE |
| BC |
| 3 |
| 5 |
| 3 |
| 5 |
| 36 |
| 5 |
| 36 |
| 5 |
| 14 |
| 5 |
| AE |
| AC |
| ||
| 10 |
| 14 |
| 50 |
| 7 |
| 25 |
| 24 |
| 25 |
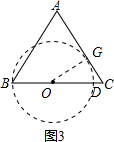
| 3 |
| 5 |
| 4 |
| 5 |
| OG |
| OC |
| R |
| 12-R |
| 4 |
| 5 |
| 16 |
| 3 |
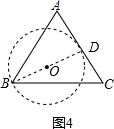
| BD |
| BC |
| 2R |
| 12 |
| 4 |
| 5 |
| 24 |
| 5 |
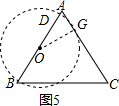
| OG |
| OA |
| R |
| 10-R |
| 24 |
| 25 |
| 240 |
| 49 |


科目:初中数学 来源: 题型:
| A、1.37×108米 |
| B、14×107米 |
| C、13.7×107米 |
| D、1.4×108米 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,边长为5km的正方形网格表示海平面示意图,其中阴影部分表示轮船无法通过的海域,甲轮船从A码头出发沿北偏东45°方向以10km/h的速度行驶20
如图,边长为5km的正方形网格表示海平面示意图,其中阴影部分表示轮船无法通过的海域,甲轮船从A码头出发沿北偏东45°方向以10km/h的速度行驶20| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,将一块斜边长为12cm,∠B=60°的直角三角板ABC,绕点C沿逆时针方向旋转90°至△′B′C′的位置,再沿CB向右平移,使点B′刚好落在斜边AB上,那么此三角板向右平移的距离是( )
如图,将一块斜边长为12cm,∠B=60°的直角三角板ABC,绕点C沿逆时针方向旋转90°至△′B′C′的位置,再沿CB向右平移,使点B′刚好落在斜边AB上,那么此三角板向右平移的距离是( )A、6-2
| ||
B、2
| ||
C、4-
| ||
| D、3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知一次函数y=kx+b的图象经过点A(1,0),与反比例函数y=
如图,已知一次函数y=kx+b的图象经过点A(1,0),与反比例函数y=| m |
| x |
| m |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com