
����Ŀ����ͼ1����ƽ��ֱ������ϵ![]() �У�һ�κ���
�У�һ�κ���![]() ��
��![]() �ᡢ
�ᡢ![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ���㣬
���㣬![]() ��ĸ�������һ��
��ĸ�������һ��![]() ��
��![]() �������������һ��
�������������һ��![]() ��
��![]()
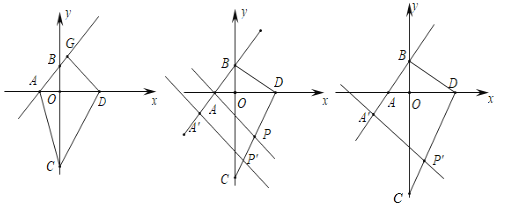
��1����ͼ1����ֱ��![]() ����һ��Ϊ
����һ��Ϊ![]() ���߶�
���߶�![]() ����
����![]() ʼ���ڵ�
ʼ���ڵ�![]() ����ࣩ�����߶�
����ࣩ�����߶�![]() ��ֱ��
��ֱ��![]() ƽ�Ƶõ��߶�
ƽ�Ƶõ��߶�![]() ��ʹ���ı���
��ʹ���ı���![]() ���ܳ���С��������ı���
���ܳ���С��������ı���![]() �ܳ�����Сֵ�ʹ�ʱ��
�ܳ�����Сֵ�ʹ�ʱ��![]() �����꣮
�����꣮
��2����ͼ2����![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() ��
��![]() �㣬��ֱ��
�㣬��ֱ��![]() ��ֱ��
��ֱ��![]() ƽ�ƣ�ƽ�ƺ���ֱ��
ƽ�ƣ�ƽ�ƺ���ֱ��![]() ��
��![]() �Ľ���ֱ���
�Ľ���ֱ���![]() ��
��![]() �����ʣ���ֱ��
�����ʣ���ֱ��![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ
��ʹ![]() �ǵ��������Σ������ڣ������ʱ��������������
�ǵ��������Σ������ڣ������ʱ��������������![]() ������Ӧ��
������Ӧ��![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1���ı���CDG'F'�ܳ�����СֵΪ3![]() +2
+2![]() +
+![]() ��G'��-7��1������2�����ڣ�A'��-2��-1����A'��-
��G'��-7��1������2�����ڣ�A'��-2��-1����A'��-![]() ��-
��-![]() ����A'��1+
����A'��1+![]() ��2+
��2+![]() ����A'��-2-
����A'��-2-![]() ��-1-
��-1-![]() ��
��
��������
��1��������ɵã�A��-1��0����B��0��1����C��0��-6����D��3��0��������D��DN��AB������F'��F'N��DG'������C����ֱ��AB�ĶԳƵ�G'������G'N��AB�Ľ���ΪF'����ʱG'D=F'N��G'F'=F'C���ı���CDG'F'�ܳ�=CD+F'G'+CF'+G'D=3![]() +2
+2![]() +F'G'+F'N=3
+F'G'+F'N=3![]() +2
+2![]() +G'N�����AB�Ľ���ʽΪy=x+1��DN��ֱ�߽���ʽΪy=x-3�����N��1��-2����G'��-7��1������G'N=
+G'N�����AB�Ľ���ʽΪy=x+1��DN��ֱ�߽���ʽΪy=x-3�����N��1��-2����G'��-7��1������G'N=![]() �������ı���CDG'F'�ܳ�����СֵΪ3
�������ı���CDG'F'�ܳ�����СֵΪ3![]() +2
+2![]() +
+![]() ��
��
��2�������CD��ֱ�߽���ʽΪy=2x-6����P'��m��2m-6������AP'=DP'ʱ����P��AD�Ĵ�ֱƽ�����ϣ�P'��1��-4������AD=AP'ʱ��16=��m+1��2+��2m-6��2��P'��![]() ��
��![]() ������AD=DP'ʱ��16=��m-3��2+��2m-6��2��P'��3+
������AD=DP'ʱ��16=��m-3��2+��2m-6��2��P'��3+![]() ��
��![]() ����P'��3-
����P'��3-![]() ��
��![]() �������ֱ��AP�Ľ���ʽ������ƽ�ƺ�P'���������ֱ��A'P'�Ľ���ʽ���ݴ����A'�����꼴�ɣ�
�������ֱ��AP�Ľ���ʽ������ƽ�ƺ�P'���������ֱ��A'P'�Ľ���ʽ���ݴ����A'�����꼴�ɣ�
��1��������ɵã�A��-1��0����B��0��1����
��C��0��-6����tan��OCD=![]() ��
��
��D��3��0����
��CD=3![]() ��
��
��FG=2![]() ��
��
��F'G'=2![]() ��
��
����D��DN��AB������F'��F'N��DG'������C����ֱ��AB�ĶԳƵ�G'������G'N��AB�Ľ���ΪF'��
��ʱG'D=F'N��G'F'=F'C��
���ı���CDG'F'�ܳ�=CD+F'G'+CF'+G'D=3![]() +2
+2![]() +F'G'+F'N=3
+F'G'+F'N=3![]() +2
+2![]() +G'N��
+G'N��
AB�Ľ���ʽΪy=x+1��
��DN��ֱ�߽���ʽΪy=x-3��
��ND=2![]() ��
��
��N��1��-2����
G'��-7��1����
��G'N=![]() ��
��
���ı���CDG'F'�ܳ�����СֵΪ3![]() +2
+2![]() +
+![]() ��
��
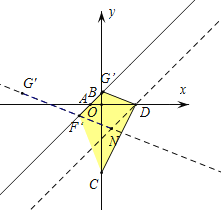
��2�����ڣ�
��ֱ��CD�Ľ���ʽΪ��![]() ��
��
����C��0��-6����D��3��0���ã�
![]() �� ��ã�
�� ��ã�![]()
��CD��ֱ�߽���ʽΪy=2x-6����P'��m��2m-6����
��AP��AB��
��AP����ֱ�߽���ʽΪy=-x-1��
��AP'=DP'ʱ����P��AD�Ĵ�ֱƽ�����ϣ�
��P'��1��-4����
��ֱ��A'P'��ֱ��APƽ�Ƶõ���
����ֱ��A'P'�Ľ���ʽΪ��y=-x+b1������P'��1��-4���ã�b1=-3
��A'P'��ֱ�߽���ʽΪy=-x-3��
����������![]() ����ã�
����ã�![]()
��A'��-2��-1����
��AD=AP'ʱ��16=��m+1��2+��2m-6��2��
��m=3��m=![]() ��
��
��P'��3��0�����ᣩ��P'��![]() ��
��![]() ����
����
ͬ�Ϸ����ɵã�
��A'P'��ֱ�߽���ʽΪy=-x-![]() ��
��
��A'��-![]() ��-
��-![]() ����
����
��AD=DP'ʱ��16=��m-3��2+��2m-6��2��
��m=3+![]() ��m=3-
��m=3-![]() ��
��
��P'��3+![]() ��
��![]() ����P'��3-
����P'��3-![]() ��-
��-![]() ����
����
ͬ�Ϸ����ɵã�
��AP'��ֱ�߽���ʽΪy=-x+3+![]() ��y=-x-3-
��y=-x-3-![]() ��
��
��A'��1+![]() ��2+
��2+![]() ����A'��-2-
����A'��-2-![]() ��-1-
��-1-![]() ����
����
��������A'��-2��-1����A'��-![]() ��-
��-![]() ����A'��1+
����A'��1+![]() ��2+
��2+![]() ����A'��-2-
����A'��-2-![]() ��-1-
��-1-![]() ����
����


 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д� ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C����DΪ���㣮
��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C����DΪ���㣮
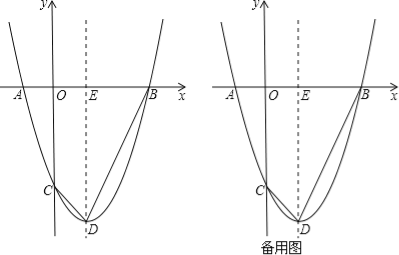
��1�����B����D�����꣮
��2������BD��CD�������ߵĶԳ�����x�ύ�ڵ�E��
�����߶�BD��һ��P��ʹ��DCP=��BDE�����P�����꣮
������������һ��M����MN��CD����ֱ��CD�ڵ�N��ʹ��CMN=��BDE�����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ y=a![]() +bx+c �ĶԳ���Ϊֱ�� x=2���� x ���һ����������Ϊ��4��0���䲿��ͼ����ͼ��ʾ�����н������н�����ȷ���ǣ� ��
+bx+c �ĶԳ���Ϊֱ�� x=2���� x ���һ����������Ϊ��4��0���䲿��ͼ����ͼ��ʾ�����н������н�����ȷ���ǣ� ��
�������߹�ԭ�㣻��4a+b=0����a��b+c��0�����������ߵĶ�������Ϊ(2��b)���ݵ� x��2 ʱ��y �� x ���������
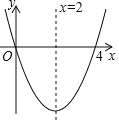
A.�٢ڢ�B.�ۢܢ�C.�٢ڢ�D.�٢ܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽����ѧ��ÿ����У�������ʱ��(��λ:![]() )����������˸�У�IJ��ֳ���ѧ�������ݵ����������Ƴ����µ�ͳ��ͼ1��ͼ2������������Ϣ�������������:
)����������˸�У�IJ��ֳ���ѧ�������ݵ����������Ƴ����µ�ͳ��ͼ1��ͼ2������������Ϣ�������������:
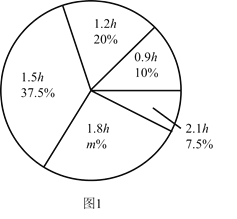
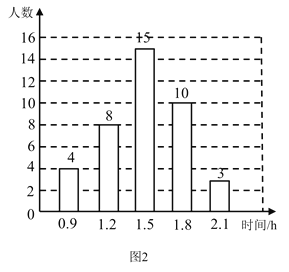
���������ν��ܵ���ij���ѧ������Ϊ ��ͼ1��![]() ��ֵΪ ��
��ֵΪ ��
��������ͳ�Ƶ�����ÿ����У�����ʱ�����ݵ�ƽ��������������λ����
����������ͳ�Ƶ�����ÿ����У�����ʱ�����������,����У����1200������ѧ�������Ƹ�Уÿ����У�����ʱ�����![]() ��ѧ��������
��ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
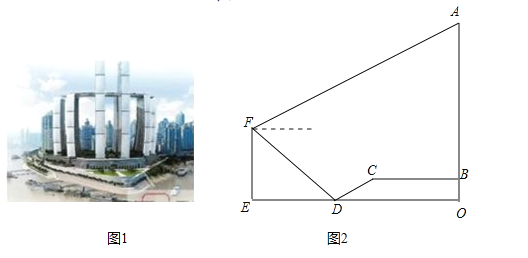
����Ŀ�������ţ���������ǵ���Դ�أ�Ҳ����δ��֮�ǡ�����ʿ�㳡��ͣ��֮�أ��㳡�ϰ˴���¥��ˮ���������£������������Ϊ�����µĵر��Խ��������������������ʿ�㳡![]() ��¥��оͲ��
��¥��оͲ��![]() ��
��![]() ��
��![]() ����ɽṹ�ⶥ���߶�ˢ�������������ߣ�С��Ϊ�˲���
����ɽṹ�ⶥ���߶�ˢ�������������ߣ�С��Ϊ�˲���![]() �ĸ߶ȣ�������¥�ײ�
�ĸ߶ȣ�������¥�ײ�![]() �������ع㳡ǰ��
�������ع㳡ǰ��![]() ������
������![]() ���̶����¶�Ϊ
���̶����¶�Ϊ![]() ��б��������
��б��������![]() ������ͷ
������ͷ![]() ��Ȼ���ڸ����ϼ���ǰ��
��Ȼ���ڸ����ϼ���ǰ��![]() ����Ѳ��
����Ѳ��![]() ����
����![]() ��С���������˿�����������˿������������
��С���������˿�����������˿������������![]() �����Ϸ���
�����Ϸ���![]() ʱ�������ͷ
ʱ�������ͷ![]() �ĸ���Ϊ
�ĸ���Ϊ![]() ��¥��
��¥��![]() ������Ϊ
������Ϊ![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��ͬһƽ���ڣ���
��ͬһƽ���ڣ���![]() ��¥
��¥![]() �ĸ߶�ԼΪ���٣��������ȷ��
�ĸ߶�ԼΪ���٣��������ȷ��![]() �ף��ο����ݣ�
�ף��ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
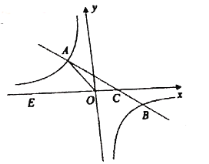
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�һ�κ���
�У�һ�κ���![]() (
(![]() )��ͼ���뷴��������
)��ͼ���뷴��������![]() (
(![]() )��ͼ���ڶ����������ڵ�
)��ͼ���ڶ����������ڵ�![]() ���㣬��
���㣬��![]() �ύ��
�ύ��![]() �㣬��
�㣬��![]() ������Ϊ
������Ϊ![]() ���߶�
���߶�![]() ��
��![]() Ϊ
Ϊ![]() ����һ�㣬
����һ�㣬![]() ��
��![]() ��
��
��1����÷�����������һ�κ����Ľ���ʽ��
��2������![]() ����
����![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ��
��![]() ��
��![]() ���ϵ����ߣ���
���ϵ����ߣ���![]() ������
������![]() ��.
��.
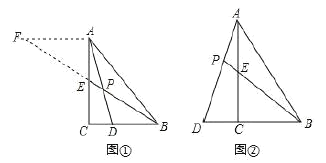
����:��ͼ�٣���![]() ��
��![]() ���ϣ�
���ϣ�![]() ��
��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ������
������![]() ��
��![]() ����
����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ����
����![]() ��ֵΪ .
��ֵΪ .
̽��:��ͼ�ڣ���![]() ��
��![]() ���ӳ����ϣ�
���ӳ����ϣ�![]() ��
��![]() ���ӳ��߽��ڵ�
���ӳ��߽��ڵ�![]() ��
�� ![]() ����
����![]() ��ֵ.
��ֵ.
Ӧ��:��̽���������£���![]() ��
��![]() ����
����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ�AD��Բ���У�������ͼ�У������̶ȵ�ֱ�߰�Ҫ��ͼ.
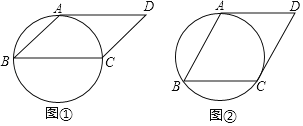
��1����BC��Բ��ֱ��������ƽ���ı���ABCD�ı�CD�ϵĸߣ�
��2����CD��Բ���У�����ƽ���ı���ABCD�ı�BC�ϵĸ�AE.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵��ڽ���2�µ���ÿ��23Ԫ�ijɱ����չ�һ��ũ��Ʒ���������ۣ�����ũ��Ʒ�ۼ�Ϊÿ��36Ԫʱ��3�·�����125����4��5�·ݸ�ũ��Ʒʮ�ֳ����������������߸�.���ۼ۲���Ļ����ϣ�5�·ݵ��������ﵽ180��.��4��5������������������ƽ�������ʲ���.
��1����4��5������������������ƽ�������ʣ�
��2��6�·��𣬸��̵���ý��۴����ķ�ʽ�����˿ͣ������鷢�֣���ũ��Ʒÿ����1Ԫ/��������������4������ũ��Ʒÿ�����۶���Ԫʱ�����̵�6�·ݻ���1920Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com