
【题目】抛物线![]() 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.
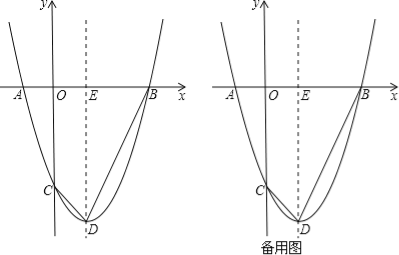
(1)求点B及点D的坐标.
(2)连结BD,CD,抛物线的对称轴与x轴交于点E.
①若线段BD上一点P,使∠DCP=∠BDE,求点P的坐标.
②若抛物线上一点M,作MN⊥CD,交直线CD于点N,使∠CMN=∠BDE,求点M的坐标.
【答案】(1)B的坐标为(3,0) D的坐标为(1,-4)
(2)①点P的坐标为(![]() ,
,![]() )②点M坐标为(
)②点M坐标为(![]() )或(5,12)
)或(5,12)
【解析】
解:(1)∵抛物线![]() 与x轴交于A,B两点(点A在点B左侧),
与x轴交于A,B两点(点A在点B左侧),
∴当y=0时,![]() ,解得x=3或x=﹣1.∴点B的坐标为(3,0).
,解得x=3或x=﹣1.∴点B的坐标为(3,0).
∵![]() ,∴顶点D的坐标为(1,-4).
,∴顶点D的坐标为(1,-4).
(2)①如图,
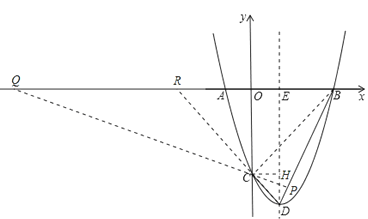
∵抛物线![]() 与y轴交于点C,
与y轴交于点C,
∴C点坐标为(0,-3).
∵对称轴为直线x=1,
∴点E的坐标为(1,0).
连接BC,过点C作CH⊥DE于H,则H点坐标为(1,﹣3),
∴CH=DH=1.
∴∠CDH=∠BCO=∠BCH=45°.
∴CD=![]() ,CB=3
,CB=3![]() ,△BCD为直角三角形.
,△BCD为直角三角形.
分别延长PC、DC,与x轴相交于点Q,R.
∵∠BDE=∠DCP=∠QCR,
∠CDB=∠CDE+∠BDE=45°+∠DCP,∠QCO=∠RCO+∠QCR=45°+∠DCP,
∴∠CDB=∠QCO.∴△BCD∽△QOC.∴![]() .
.
∴OQ=3OC=9,即Q(﹣9,0).
∴直线CQ的解析式为![]() .
.
又直线BD的解析式为![]() ,
,
由方程组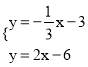 解得:
解得: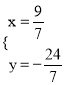 .
.
∴点P的坐标为(![]() ,
,![]() ).
).
②(Ⅰ)当点M在对称轴右侧时,
若点N在射线CD上,如图,
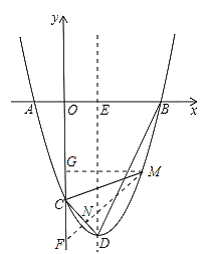
延长MN交y轴于点F,过点M作MG⊥y轴于点G.,
∵∠CMN=∠BDE,∠CNM=∠BED=90°,
∴△MCN∽△DBE.∴![]() .∴MN=2CN.
.∴MN=2CN.
设CN=a,则MN=2a.
∵∠CDE=∠DCF=45°,
∴△CNF,△MGF均为等腰直角三角形.
∴NF=CN=a,CF=![]() a.∴MF=MN+NF=3a.∴MG=FG=
a.∴MF=MN+NF=3a.∴MG=FG=![]() a.
a.
∴CG=FG﹣FC=![]() a.
a.
∴M(![]() a,
a,![]() ).
).
代入抛物线![]() ,解得a=
,解得a=![]() .,
.,
∴M(![]() ).
).
若点N在射线DC上,如图,
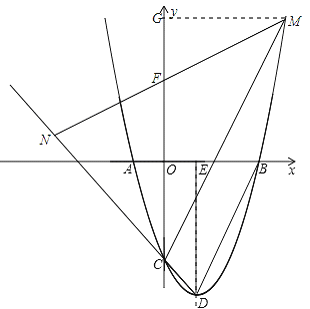
MN交y轴于点F,过点M作MG⊥y轴于点G,
∵∠CMN=∠BDE,∠CNM=∠BED=90°,
∴△MCN∽△DBE,∴![]() .
.
∴MN=2CN..
设CN=a,则MN=2a.
∵∠CDE=45°,
∴△CNF,△MGF均为等腰直角三角形.,
∴NF=CN=a,CF=![]() a.
a.
∴MF=MN﹣NF=a,∴MG=FG=![]() a.∴CG=FG+FC=
a.∴CG=FG+FC=![]() a.∴M(
a.∴M(![]() a,
a,![]() ).
).
代入抛物线![]() ,解得a=
,解得a=![]() .
.
∴M(5,12).
(Ⅱ)当点M在对称轴左侧时,
∵∠CMN=∠BDE<45°,∴∠MCN>45°.
而抛物线左侧任意一点K,都有∠KCN<45°,∴点M不存在.
综上可知,点M坐标为(![]() )或(5,12).
)或(5,12).
(1)解方程![]() ,求出x=3或﹣1,根据抛物线
,求出x=3或﹣1,根据抛物线![]() 与x轴交于A,B两点(点A在点B左侧),确定点B的坐标为(3,0);将抛物线写成顶点式
与x轴交于A,B两点(点A在点B左侧),确定点B的坐标为(3,0);将抛物线写成顶点式![]() ,即可确定顶点D的坐标.
,即可确定顶点D的坐标.
(2)①根据抛物线![]() ,得到点C、点E的坐标.连接BC,过点C作CH⊥DE于H,由勾股定理得出CD=
,得到点C、点E的坐标.连接BC,过点C作CH⊥DE于H,由勾股定理得出CD=![]() ,CB=3
,CB=3![]() ,证明△BCD为直角三角形.分别延长PC、DC,与x轴相交于点Q,R.根据两角对应相等的两三角形相似证明△BCD∽△QOC,则
,证明△BCD为直角三角形.分别延长PC、DC,与x轴相交于点Q,R.根据两角对应相等的两三角形相似证明△BCD∽△QOC,则![]() ,得出Q的坐标(﹣9,0),运用待定系数法求出直线CQ的解析式为
,得出Q的坐标(﹣9,0),运用待定系数法求出直线CQ的解析式为![]() ,直线BD的解析式为
,直线BD的解析式为![]() ,解方程组
,解方程组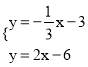 ,即可求出点P的坐标.
,即可求出点P的坐标.
②分点M在对称轴右侧和点M在对称轴左侧两种情况进行讨论:(Ⅰ)当点M在对称轴右侧时,分点N在射线CD上和点N在射线DC上两种情况讨论;(Ⅱ)当点M在对称轴左侧时,由于∠BDE<45°,得到∠CMN<45°,根据直角三角形两锐角互余得出∠MCN>45°,而抛物线左侧任意一点K,都有∠KCN<45°,所以点M不存在.


科目:初中数学 来源: 题型:
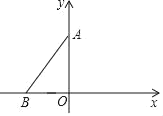
【题目】如图,在平面直角坐标系中,点A(0,4)、B(﹣3,0),将线段AB沿x轴正方向平移n个单位得到菱形ABCD.
(1)画出菱形ABCD,并直接写出n的值及点D的坐标;
(2)已知反比例函数y=![]() 的图象经过点D,ABMN的顶点M在y轴上,N在y=
的图象经过点D,ABMN的顶点M在y轴上,N在y=![]() 的图象上,求点M的坐标;
的图象上,求点M的坐标;
(3)若点A、C、D到某直线l的距离都相等,直接写出满足条件的直线解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
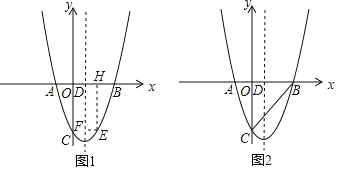
【题目】如图,抛物线y=x2﹣4x﹣5与x轴交于A,B两点(电B在点A的右侧),与y轴交于点C,抛物线的对称轴与x轴交于点D.
(1)求A,B,C三点的坐标及抛物线的对称轴.
(2)如图1,点E(m,n)为抛物线上一点,且2<m<5,过点E作EF∥x轴,交抛物线的对称轴于点F,作EH⊥x轴于点H,求四边形EHDF周长的最大值.
(3)如图2,点P为抛物线对称轴上一点,是否存在点P,使以点P,B,C为顶点的三角形是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
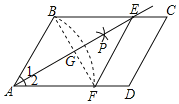
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,则四边形ABEF的面积是___.
BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,则四边形ABEF的面积是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天220元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.设每个房间每天的定价增加x元.
求:(1)房间每天的入住量y(间)关于x(元)的函数关系式;
(2)设该宾馆客房部每天的利润为w(元),当每个房间的定价为每天多少元时,w有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=﹣![]() x+2的图象,绕x轴上一点P(m,0)旋转180°,所得的图象经过(0.﹣1),则m的值为( )
x+2的图象,绕x轴上一点P(m,0)旋转180°,所得的图象经过(0.﹣1),则m的值为( )
A.﹣2B.﹣1C.1D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 与
与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() 两点,
两点,![]() 轴的负半轴上一点
轴的负半轴上一点![]() ,
,![]() 轴的正半轴上有一点
轴的正半轴上有一点![]() 且
且![]()
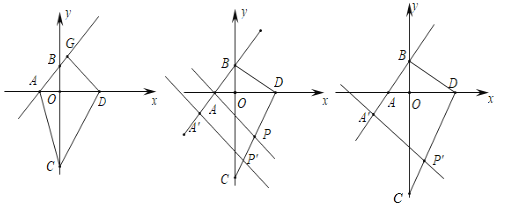
(1)如图1,在直线![]() 上有一长为
上有一长为![]() 的线段
的线段![]() (点
(点![]() 始终在点
始终在点![]() 的左侧),将线段
的左侧),将线段![]() 沿直线
沿直线![]() 平移得到线段
平移得到线段![]() ,使得四边形
,使得四边形![]() 的周长最小,请求出四边形
的周长最小,请求出四边形![]() 周长的最小值和此时点
周长的最小值和此时点![]() 的坐标.
的坐标.
(2)如图2,过![]() 作直线
作直线![]() 交直线
交直线![]() 与
与![]() 点,将直线
点,将直线![]() 沿直线
沿直线![]() 平移,平移后与直线
平移,平移后与直线![]() 、
、![]() 的交点分别是
的交点分别是![]() ,
,![]() .请问,在直线
.请问,在直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 是等腰三角形?若存在,求出此时符合条件的所有
是等腰三角形?若存在,求出此时符合条件的所有![]() 点所对应的
点所对应的![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com