
【题目】某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天220元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.设每个房间每天的定价增加x元.
求:(1)房间每天的入住量y(间)关于x(元)的函数关系式;
(2)设该宾馆客房部每天的利润为w(元),当每个房间的定价为每天多少元时,w有最大值?最大值是多少?
【答案】(1)![]() ;(2)当每个房间的定价为每天420元时,w有最大值,且最大值是16000元.
;(2)当每个房间的定价为每天420元时,w有最大值,且最大值是16000元.
【解析】
(1)根据每个房间每天的定价每增加10元时,就会有一个房间空闲,这个规律即可列出房间每天的入住量y(间)关于x(元)的函数关系式;
(2)根据利润等于总收入减去总成本列出w关于x 的二次函数关系,即可根据二次函数的性质求出w的最小值.
解:(1)∵当每个房间每天的定价每增加10元时,就会有一个房间空闲,
∴每个房间每天的定价增加x元,有![]() 个房间空闲
个房间空闲
∴房间每天的入住量y(间)关于x(元)的函数关系式为:![]() .
.
(2)![]()
∴![]()
![]()
∵![]() >0,
>0,
∴当![]() 时,w有最大值16000,
时,w有最大值16000,
此时,![]() ,
,
答:当每个房间的定价为每天420元时,w有最大值,且最大值是16000元.


科目:初中数学 来源: 题型:
【题目】如图是张亮、李娜两位同学零花钱全学期各项支出的统计图.根据统计图,下列对两位同学购买书籍支出占全学期总支出的百分比作出的判断中,正确的是( )


A. 张亮的百分比比李娜的百分比大 B. 张娜的百分比比张亮的百分比大
C. 张亮的百分比与李娜的百分比一样大 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在现实生活中,我们会看到许多“标准”的矩形,如我们的课本封面、A4的打印纸等,其实这些矩形的长与宽之比都为![]() :1,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形”ABCD中,P为DC边上一定点,且CP=BC,如图所示.
:1,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形”ABCD中,P为DC边上一定点,且CP=BC,如图所示.

(1)如图①,求证:BA=BP;
(2)如图②,点Q在DC上,且DQ=CP,若G为BC边上一动点,当△AGQ的周长最小时,求![]() 的值;
的值;
(3)如图③,已知AD=1,在(2)的条件下,连接AG并延长交DC的延长线于点F,连接BF,T为BF的中点,M、N分别为线段PF与AB上的动点,且始终保持PM=BN,请证明:△MNT的面积S为定值,并求出这个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数![]() ,下列说法正确的个数是( )
,下列说法正确的个数是( )
①函数图象位于第一、三象限;②函数值 y 随 x 的增大而减小;③若 A(-1,![]() ),B(2,
),B(2,![]() ),C(1,
),C(1,![]() )是图象上三个点,则
)是图象上三个点,则![]() <
<![]() <
<![]() ;④P 为图象上任一点,过 P 作 PQ⊥y 轴于点 Q,则△OPQ 的面积是定值.
;④P 为图象上任一点,过 P 作 PQ⊥y 轴于点 Q,则△OPQ 的面积是定值.
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.
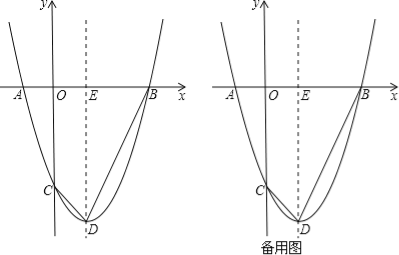
(1)求点B及点D的坐标.
(2)连结BD,CD,抛物线的对称轴与x轴交于点E.
①若线段BD上一点P,使∠DCP=∠BDE,求点P的坐标.
②若抛物线上一点M,作MN⊥CD,交直线CD于点N,使∠CMN=∠BDE,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点P为AB边上任一点,过P分别作PE⊥AC于E,PF⊥BC于F,则线段EF的最小值是__________.
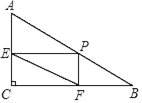
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小华和同伴在春游期间,发现在某地小山坡的点E处有一棵盛开的桃花的小桃树,他想利用平面镜测量的方式计算一下小桃树到山脚下的距离,即DE的长度,小华站在点B的位置,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E,且BC=2.7米,CD=11.5米,∠CDE=120°,已知小华的身高为1.8米,请你利用以上的数据求出DE的长度.(结果保留根号)
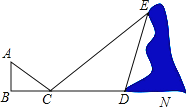
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() (
(![]() )的图象与反比例函数
)的图象与反比例函数![]() (
(![]() )的图象交于二、四象限内的
)的图象交于二、四象限内的![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 的坐标为
的坐标为![]() .线段
.线段![]() ,
,![]() 为
为![]() 轴上一点,
轴上一点,![]() ,
,![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)连接![]() ,求
,求![]() 的面积.
的面积.
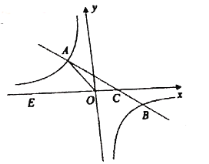
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com