
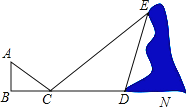
����Ŀ����ͼ��С����ͬ���ڴ����ڼ䣬������ij��Сɽ�µĵ�E����һ��ʢ�����һ���С��������������ƽ�澵�����ķ�ʽ����һ��С������ɽ���µľ��룬��DE�ij��ȣ�С��վ�ڵ�B��λ�ã���ͬ���ƶ�ƽ�澵����C������ʱС����ƽ�澵�ڿ��Կ�����E����BC��2.7�ף�CD��11.5�ף���CDE��120�㣬��֪С��������Ϊ1.8�ף������������ϵ��������DE�ij��ȣ�������������ţ�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
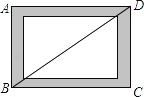
����Ŀ����ͼ��С��Ϊ�������ı��εIJ��ȶ��ԣ����ĸ�ľ���ö��Ӷ���һ�����ο��ABCD��B��D����֮����һ����Ƥ����ֱ�̶���Ȼ������Ť����ܣ��۲������ı��εı仯�������жϴ�����ǣ� ��
A. �ı���ABCD�ɾ��α�Ϊƽ���ı��� B. BD�ij�������
C. �ı���ABCD��������� D. �ı���ABCD���ܳ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ݿͷ�����60�����乩�ο;�ס����ÿ������Ķ���Ϊÿ��220Ԫʱ���������ס������ÿ������ÿ��Ķ���ÿ����10Ԫʱ���ͻ���һ��������У������ο���ס�ķ��䣬�������ÿ������ÿ��֧��20Ԫ�ĸ��ַ��ã���ÿ������ÿ��Ķ�������xԪ��
��(1)����ÿ�����ס��y(��)����x(Ԫ)�ĺ�����ϵʽ��
(2)��ñ��ݿͷ���ÿ�������Ϊw(Ԫ)����ÿ������Ķ���Ϊÿ�����Ԫʱ��w�����ֵ�����ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
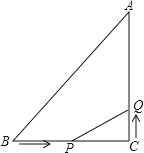
����Ŀ����ͼ����ABC �У���C=90�㣬AC=3cm��BC=4cm������ P �ӵ� B ������ 2cm/s �ٶ���� c �ƶ���ͬʱ���� Q �� C ������ 1cm/s ���ٶ���� A �ƶ��� �����ǵ��˶�ʱ��Ϊ t��
��1����������֪��CQ= ��CP= �����ú� t �Ĵ���ʽ��ʾ��
��2��t Ϊ��ֵʱ����CPQ ��������ڡ�ABC �����![]() ��
��
��3���˶�����ʱ����CPQ ���CBA ���ƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y����![]() x+2��ͼ����x����һ��P��m��0����ת180�㣬���õ�ͼ����0����1������m��ֵΪ��������
x+2��ͼ����x����һ��P��m��0����ת180�㣬���õ�ͼ����0����1������m��ֵΪ��������
A.��2B.��1C.1D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������
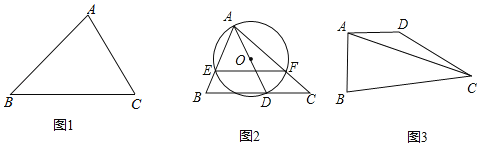
��1����ͼ1���ڡ�ABC�У���A��75�㣬��C��60�㣬AC��6![]() �����ABC�����Բ�뾶R��ֵ��
�����ABC�����Բ�뾶R��ֵ��
����̽��
��2����ͼ2���ڡ�ABC�У���BAC��60�㣬��C��45�㣬AC��8![]() ����DΪ��BC�ϵĶ��㣬����AD��ADΪֱ������O����AB��AC�ֱ��ڵ�E��F����E��F����EF����Сֵ��
����DΪ��BC�ϵĶ��㣬����AD��ADΪֱ������O����AB��AC�ֱ��ڵ�E��F����E��F����EF����Сֵ��
������
��3����ͼ3�����ı���ABCD�У���BAD��90�㣬��BCD��30�㣬AB��AD��BC+CD��12![]() ������AC���߶�AC�ij��Ƿ������Сֵ�������ڣ�����Сֵ���������ڣ���˵�����ɣ�
������AC���߶�AC�ij��Ƿ������Сֵ�������ڣ�����Сֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y1=ax+b��a��0����ͼ����y���ཻ�ڵ�A���뷴��������y2=![]() ��c��0����ͼ���ཻ�ڵ�B��3��2����C����1��n����
��c��0����ͼ���ཻ�ڵ�B��3��2����C����1��n����
��1����һ�κ����ͷ����������Ľ���ʽ��
��2������ͼ��ֱ��д��y1��y2ʱx��ȡֵ��Χ��
��3����y�����Ƿ���ڵ�P��ʹ��PABΪֱ�������Σ�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�Ƴ�һ���²�Ʒ��ͨ���г����к�������ɫ�ܻ�ӭ�ij̶ȷֱ��A��ɫ��B��ɫ��C��ɫ�IJ�Ʒ�ڳɱ��Ļ����Ϸֱ�Ӽ�40%��50%��60%���ۣ�������ɫ��Ʒ�ijɱ�һ����������һ�����ȵľ�Ӫ����C��ɫ��Ʒ������ռ��������40%��������ɫ��Ʒ����������Ϊ51.5%���ڶ������ȣ���˾������A��Ʒ����������������A��Ʒ�ijɱ������25%�������������60%��������Ϊԭ����������B��Ʒ��������ߵ����������A��Ʒ������һ����C��Ʒ�������ȵ�һ���������50%����ڶ������ȵ���������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC��OΪ��AC��һ�㣨�����A��C�غϣ�����OCΪ�뾶��Բ�ֱ�BC��AC�ڵ�D��E������D��DF��AB�ڵ�F.
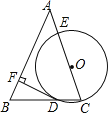
��1����֤��ֱ��DF�ǡ�O�����ߣ�
��2������A��45����OC��2�����ӻ�![]() �ij�.�������������
�ij�.�������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com