
【题目】问题提出
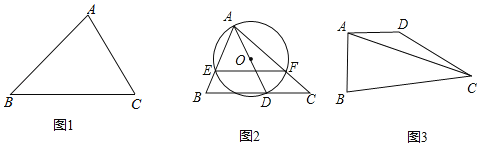
(1)如图1,在△ABC中,∠A=75°,∠C=60°,AC=6![]() ,求△ABC的外接圆半径R的值;
,求△ABC的外接圆半径R的值;
问题探究
(2)如图2,在△ABC中,∠BAC=60°,∠C=45°,AC=8![]() ,点D为边BC上的动点,连接AD以AD为直径作⊙O交边AB、AC分别于点E、F,接E、F,求EF的最小值;
,点D为边BC上的动点,连接AD以AD为直径作⊙O交边AB、AC分别于点E、F,接E、F,求EF的最小值;
问题解决
(3)如图3,在四边形ABCD中,∠BAD=90°,∠BCD=30°,AB=AD,BC+CD=12![]() ,连接AC,线段AC的长是否存在最小值,若存在,求最小值:若不存在,请说明理由.
,连接AC,线段AC的长是否存在最小值,若存在,求最小值:若不存在,请说明理由.
【答案】(1)△ABC的外接圆的R为6;(2)EF的最小值为12;(3)存在,AC的最小值为9![]() .
.
【解析】
(1)如图1中,作△ABC的外接圆,连接OA,OC.证明∠AOC=90°即可解决问题;
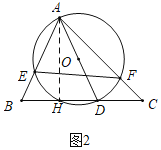
(2)如图2中,作AH⊥BC于H.当直径AD的值一定时,EF的值也确定,根据垂线段最短可知当AD与AH重合时,AD的值最短,此时EF的值也最短;
(3)如图3中,将△ADC绕点A顺时针旋转90°得到△ABE,连接EC,作EH⊥CB交CB的延长线于H,设BE=CD=x.证明EC=![]() AC,构建二次函数求出EC的最小值即可解决问题.
AC,构建二次函数求出EC的最小值即可解决问题.
解:(1)如图1中,作△ABC的外接圆,连接OA,OC.

∵∠B=180°﹣∠BAC﹣∠ACB=180°﹣75°﹣60°=45°,
又∵∠AOC=2∠B,
∴∠AOC=90°,
∴AC=6![]() ,
,
∴OA=OC=6,
∴△ABC的外接圆的R为6.
(2)如图2中,作AH⊥BC于H.
∵AC=8![]() ,∠C=45°,
,∠C=45°,
∴AH=ACsin45°=8![]() ×
×![]() =8
=8![]() ,
,
∵∠BAC=60°,
∴当直径AD的值一定时,EF的值也确定,
根据垂线段最短可知当AD与AH重合时,AD的值最短,此时EF的值也最短,
如图2﹣1中,当AD⊥BC时,作OH⊥EF于H,连接OE,OF.

∵∠EOF=2∠BAC=120°,OE=OF,OH⊥EF,
∴EH=HF,∠OEF=∠OFE=30°,
∴EH=OFcos30°=4![]()
![]() =6,
=6,
∴EF=2EH=12,
∴EF的最小值为12.
(3)如图3中,将△ADC绕点A顺时针旋转90°得到△ABE,连接EC,作EH⊥CB交CB的延长线于H,设BE=CD=x.

∵∠AE=AC,∠CAE=90°,
∴EC=![]() AC,∠AEC=∠ACE=45°,
AC,∠AEC=∠ACE=45°,
∴EC的值最小时,AC的值最小,
∵∠BCD=∠ACB+∠ACD=∠ACB+∠AEB=30°,
∴∠∠BEC+∠BCE=60°,
∴∠EBC=120°,
∴∠EBH=60°,
∴∠BEH=30°,
∴BH=![]() x,EH=
x,EH=![]() x,
x,
∵CD+BC=12![]() ,CD=x,
,CD=x,
∴BC=12![]() ﹣x
﹣x
∴EC2=EH2+CH2=(![]() x)2+
x)2+![]() =x2﹣12
=x2﹣12![]() x+432,
x+432,
∵a=1>0,
∴当x=﹣![]() =6
=6![]() 时,EC的长最小,
时,EC的长最小,
此时EC=18,
∴AC=![]() EC=9
EC=9![]() ,
,
∴AC的最小值为9![]() .
.


科目:初中数学 来源: 题型:
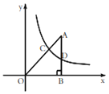
【题目】如图,在平面直角坐标系中,O为坐标原点,![]() 的边
的边![]() 垂直于
垂直于![]() 轴,垂足为B,反比例函数
轴,垂足为B,反比例函数![]() 的图象经过AO上的点C,且
的图象经过AO上的点C,且![]() ,与边AB相交于点D,
,与边AB相交于点D, ![]() .
.
(1)求点C的横坐标;
(2)求反比例函数![]() 的解析式;
的解析式;
(3)求经过C,D两点的一次函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商场经销一种高档水果,商场为了在中秋节和国庆节期间扩大销量,将售价从原来的每千克40元经两次调价后调至每千克32.4元.
(1)若该商场两次调次的降价率相同,求这个降价率;
(2)现在假期结束了,商场准备适当涨价,如果现在每千克盈利10元,每天可售出500千克,经市场调查发现,在进货不变的情况下,若每千克涨价1元,日销量将减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
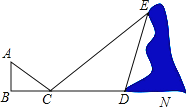
【题目】如图,小华和同伴在春游期间,发现在某地小山坡的点E处有一棵盛开的桃花的小桃树,他想利用平面镜测量的方式计算一下小桃树到山脚下的距离,即DE的长度,小华站在点B的位置,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E,且BC=2.7米,CD=11.5米,∠CDE=120°,已知小华的身高为1.8米,请你利用以上的数据求出DE的长度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)求第一批悠悠球每套的进价是多少元;
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于25%,那么每套悠悠球的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】相传,唐高祖年间,大将军李靖在八月十五征讨匈奴得胜,凯旋而归.当时有经商的吐鲁番人向唐朝皇帝献饼祝捷.高祖李渊接过华丽的饼盒,拿出圆饼,笑指空中明月说:“应将胡饼邀蟾蜍”.说完把饼分给群臣一起吃.从此后,月饼的制作越来越考究.“月是故乡明,饼表思亲情”,现在,每年的中秋佳节月饼成了人们必备佳肴.今年中秋,某超市主打广式月饼和苏式月饼.已知一盒广式月饼比苏式月饼贵14元,买3盒广式月饼和2盒苏式月饼共472元.
(1)求1盒广式月饼和1盒苏式月饼各多少钱;
(2)今年中秋节前夕,通过调查,发现广式月饼受大众青睐.于是,一广告公司计划购买一批广式月饼作为中秋节礼物送给单位一部分员工.该公司原计划购买广式月饼30盒.为了让更多的员工得到月饼,但又不超出预算.在与超市协商后,超市给广告公司如下优惠:若购买数量超过30盒,每盒月饼的价格下降![]() ,但购买量需要增加
,但购买量需要增加![]() ,且单价不低于苏式月饼的价格.最终,该公司用3240元购置了这批月饼,求a的值.
,且单价不低于苏式月饼的价格.最终,该公司用3240元购置了这批月饼,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点P、点Q同时从点B出发,点P以
,点P、点Q同时从点B出发,点P以![]() 的速度沿
的速度沿![]() 运动,终点为C,点Q以
运动,终点为C,点Q以![]() 的速度沿
的速度沿![]() 运动,当点P到达终点时两个点同时停止运动,设点P,Q出发t秒时,
运动,当点P到达终点时两个点同时停止运动,设点P,Q出发t秒时,![]() 的面积为
的面积为![]() ,已知y与t的函数关系的图象如图
,已知y与t的函数关系的图象如图![]() 曲线OM和MN均为抛物线的一部分
曲线OM和MN均为抛物线的一部分![]() ,给出以下结论:
,给出以下结论:![]() ;
;![]() 曲线MN的解析式为
曲线MN的解析式为![]() ;
;![]() 线段PQ的长度的最大值为
线段PQ的长度的最大值为![]() ;
;![]() 若
若![]() 与
与![]() 相似,则
相似,则![]() 秒
秒![]() 其中正确的是
其中正确的是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com