
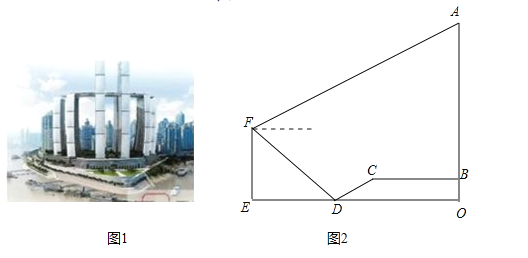
【题目】朝天门,既是重庆城的起源地,也是“未来之城”来福士广场的停泊之地,广场上八幢塔楼临水北向、错落有致,宛如轮扬帆起航,成为我市新的地标性建筑—“朝大杨帆”、来福士广场![]() 塔楼核芯筒于
塔楼核芯筒于![]() 年
年![]() 月
月![]() 日完成结构封顶,高度刷新了重庆的天际线,小明为了测量
日完成结构封顶,高度刷新了重庆的天际线,小明为了测量![]() 的高度,他从塔楼底部
的高度,他从塔楼底部![]() 出发,沿广场前进
出发,沿广场前进![]() 米至点
米至点![]() ,继而沿坡度为
,继而沿坡度为![]() 的斜坡向下走
的斜坡向下走![]() 米到达码头
米到达码头![]() ,然后在浮桥上继续前行
,然后在浮桥上继续前行![]() 米至巡船
米至巡船![]() ,在
,在![]() 处小明操作无人勘测机,当无人勘测机飞行至点
处小明操作无人勘测机,当无人勘测机飞行至点![]() 的正上方点
的正上方点![]() 时,测得码头
时,测得码头![]() 的俯角为
的俯角为![]() 、楼顶
、楼顶![]() 的仰角为
的仰角为![]() ,点
,点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 在同一平面内,则
在同一平面内,则![]() 塔楼
塔楼![]() 的高度约为多少?(结果精确到
的高度约为多少?(结果精确到![]() 米,参考数据:
米,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
【答案】334米
【解析】
作FG⊥AB于G,CH⊥OE于H,根据坡度的概念分别求出CH、DH,根据正切的定义分别求出AG、EF,结合图形计算,得到答案.
作FG⊥AB于G,CH⊥OE于H,
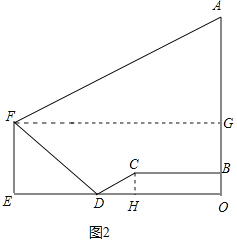
设CH=x米,
∵斜坡CD的坡度为i=1:2.4,
∴DH=2.4x,
由勾股定理得,CD2=CH2+DH2,即652=x2+(2.4x)2,
解得,x=25,
即CH=x=25,DH=2.4x=60,
∴EO=ED+DH+HO=100+60+185=345,
∴FG=EO=345,
在Rt△AFG中,tan∠AFG=![]() ,
,
∴AG=FGtan∠AFG=115![]() ,
,
在Rt△FDE中,tan∠FDE=![]() ,
,
∴EF=DEtan∠FDE≈160,
∴GO=EF=160,
∴AB=AG+GO-OB=115![]() +160-25≈334(米)
+160-25≈334(米)
答:T3N塔楼AB的高度约为334米.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
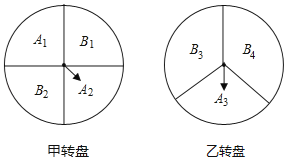
【题目】某超市在春节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣和优惠,在每个转盘中指针指向每个区域的可能性均相同,若指针指向分界线,则重新转动转盘,区域对应的优惠方式如下,A1,A2,A3区域分别对应9折8折和7折优惠,B1,B2,B3,B4区域对应不优惠?本次活动共有两种方式.
方式一:转动转盘甲,指针指向折扣区域时,所购物品享受对应的折扣优惠,指针指向其他区域无优惠;
方式二:同时转动转盘甲和转盘乙,若两个转盘的指针均指向折扣区域时,所购物品享受折上折的优惠,其他情况无优惠.
(1)若顾客选择方式一,则享受优惠的概率为 ;
(2)若顾客选择方式二,请用树状图或列表法列出所有可能顾客享受折上折优惠的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
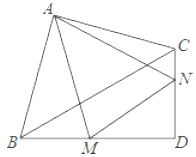
【题目】如图,在Rt△ABC和Rt△BCD中,∠BAC=∠BDC=90°,BC=4,AB=AC,∠CBD=30°,M,N分别在BD,CD上,∠MAN=45°,则△DMN的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 与
与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() 两点,
两点,![]() 轴的负半轴上一点
轴的负半轴上一点![]() ,
,![]() 轴的正半轴上有一点
轴的正半轴上有一点![]() 且
且![]()
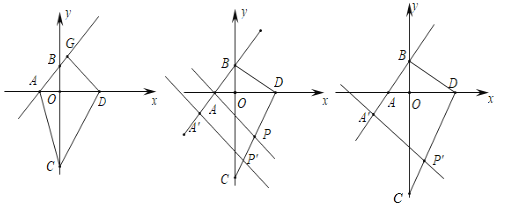
(1)如图1,在直线![]() 上有一长为
上有一长为![]() 的线段
的线段![]() (点
(点![]() 始终在点
始终在点![]() 的左侧),将线段
的左侧),将线段![]() 沿直线
沿直线![]() 平移得到线段
平移得到线段![]() ,使得四边形
,使得四边形![]() 的周长最小,请求出四边形
的周长最小,请求出四边形![]() 周长的最小值和此时点
周长的最小值和此时点![]() 的坐标.
的坐标.
(2)如图2,过![]() 作直线
作直线![]() 交直线
交直线![]() 与
与![]() 点,将直线
点,将直线![]() 沿直线
沿直线![]() 平移,平移后与直线
平移,平移后与直线![]() 、
、![]() 的交点分别是
的交点分别是![]() ,
,![]() .请问,在直线
.请问,在直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 是等腰三角形?若存在,求出此时符合条件的所有
是等腰三角形?若存在,求出此时符合条件的所有![]() 点所对应的
点所对应的![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,以
中,以![]() 为斜边,作直角
为斜边,作直角![]() ,使点
,使点![]() 落在
落在![]() 内,
内,![]() .
.
(1)如图1,若![]() ,
,![]() ,
,![]() ,点
,点![]() 分别为
分别为![]() 边的中点,连接
边的中点,连接![]() ,求线段
,求线段![]() 的长;
的长;
(2)如图2,若![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转一定角度,得到
逆时针旋转一定角度,得到![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,求证:
,求证:![]() .
.

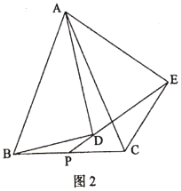
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川广安10分)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过A、B、C三点,已知点A(﹣3,0),B(0,3),C(1,0).

(1)求此抛物线的解析式.
(2)点P是直线AB上方的抛物线上一动点,(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.
①动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;
②连接PA,以AP为边作图示一侧的正方形APMN,随着点P的运动,正方形的大小、位置也随之改变.当顶点M或N恰好落在抛物线对称轴上时,求出对应的P点的坐标.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形![]() 中,
中,![]() ,连接
,连接![]() ,以
,以![]() 为直径作半圆
为直径作半圆![]() 交
交![]() 于点
于点![]() ,
,
(1)过点D作OB的垂线,垂足为E,求证:DE与半圆C相切;
(2)若![]() ,
,![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
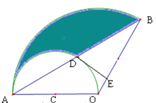
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com