
����Ŀ����2013���Ĵ��㰲10�֣���ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2+bx+c����A��B��C���㣬��֪��A����3��0����B��0��3����C��1��0����

��1����������ߵĽ���ʽ��
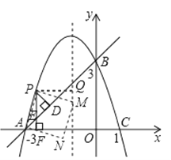
��2����P��ֱ��AB�Ϸ�����������һ���㣬�������A��B�غϣ�������P��x��Ĵ��ߣ�����ΪF����ֱ��AB�ڵ�E����PD��AB�ڵ�D��
������P��ʲôλ��ʱ����PDE���ܳ���������ʱP������ꣻ
������PA����APΪ����ͼʾһ���������APMN�����ŵ�P���˶��������εĴ�С��λ��Ҳ��֮�ı䣮������M��Nǡ�����������߶Գ�����ʱ�������Ӧ��P������꣮������������ţ�
���𰸡��⣺��1����������y=ax2+bx+c������A����3��0����B��0��3����C��1��0����
��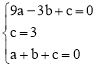 �����
�����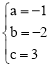 ��
��
�������ߵĽ���ʽΪy=��x2��2x+3��
��2���١�A����3��0����B��0��3������OA=OB=3�����AOB�ǵ���ֱ�������������BAO=45����
��PF��x�ᣬ���AEF=90�㩁45��=45����
����PD��AB�����PDE�ǵ���ֱ������������PDԽ����PDE���ܳ�Խ����
��ֱ��AB�Ľ���ʽΪy=x+3��
����ABƽ�е�ֱ�߽���ʽΪy=x+m��
����![]() ������y�ã�x2+3x+m��3=0��
������y�ã�x2+3x+m��3=0��
����=32��4��1����m��3��=0����m=![]() ʱ��ֱ����������ֻ��һ�����㣬PD���
ʱ��ֱ����������ֻ��һ�����㣬PD���
��ʱx=![]() ��y=
��y=![]() +
+![]() =
=![]() ��
��
����P��![]() ��
��![]() ��ʱ����PDE���ܳ������
��ʱ����PDE���ܳ������
��������y=��x2��2x+3�ĶԳ���Ϊֱ��![]() ��
��
��i����ͼ1����M�ڶԳ�����ʱ������P��PQ���Գ�����Q��
��������APMN�У�AP=PM����APM=90�㣬
���APF+��FPM=90�㣬��QPM+��FPM=90����
���APF=��QPM��
������APF����MPQ�У�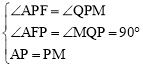 �����APF�ա�MPQ��AAS������PF=PQ��
�����APF�ա�MPQ��AAS������PF=PQ��
���P�ĺ�����Ϊn��n��0������PQ=��1��n����PF=��1��n������P������Ϊ��n����1��n����
����P��������y=��x2��2x+3�ϣ�����n2��2n+3=��1��n�������ã�n2+n��4=0��
���n1=![]() ����ȥ����n2=
����ȥ����n2=![]() ����1��n=��1��
����1��n=��1��![]() =
=![]() ��
��
����P��������![]() ��
��![]() ����
����
��ii����ͼ2����N�ڶԳ�����ʱ���������߶Գ�����x�ύ�ڵ�Q��
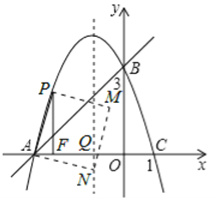
�ߡ�PAF+��FPA=90�㣬��PAF+��QAN=90�㣬���FPA=��QAN��
���ߡ�PFA=��AQN=90�㣬PA=AN�����APF�ա�NAQ��
��PF=AQ��
���P����ΪP��x����x2��2x+3����
����x2��2x+3=��1������3��=2��
���x=![]() ���������⣬��ȥ����x=
���������⣬��ȥ����x=![]() ��
��
����P������![]() ��2����
��2����
����������������Mǡ�����������߶Գ�����ʱ����P����Ϊ��![]() ��
��![]() ����������Nǡ�����������߶Գ�����ʱ����P������Ϊ��
����������Nǡ�����������߶Գ�����ʱ����P������Ϊ��![]() ��2����
��2����
����������1���ѵ�A��B��C��������������߽���ʽ�����ô���ϵ��������κ�������ʽ�����
��2�������ݵ�A��B���������OA=OB���Ӷ��õ���AOB�ǵ���ֱ�������Σ����ݵ���ֱ�������ε����ʿɵ���BAO=45�㣬Ȼ�������PED�ǵ���ֱ�������Σ����ݵ���ֱ�������ε����ʣ�PDԽ����PDE���ܳ�������жϳ�����ֱ��ABƽ�е�ֱ����������ֻ��һ������ʱ��PD��������ֱ��AB�Ľ���ʽΪy=x+3������ABƽ�е�ֱ�߽���ʽΪy=x+m���������߽���ʽ��������y���õ�����x��һԪ���η��̣����ø����б�ʽ��=0��ʽ���m��ֵ�������x��y��ֵ���Ӷ��õ���P��������
����ȷ���������ߵĶԳ��ᣬȻ��i���ֵ�M�ڶԳ�����ʱ������P��PQ���Գ�����Q������ͬ�ǵ������������APF=��QPM�������á��ǽDZߡ�֤����APF����MPQȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�PF=PQ�����P�ĺ�����Ϊn����ʾ��PQ�ij�����PF��Ȼ����������߽���ʽ���㼴�ɵý⣻��ii����N�ڶԳ�����ʱ��ͬ�������APF����ANQȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�PF=AQ�����ݵ�A�����������P�������꣬�ٴ��������߽���ʽ��������꣬���ɵõ���P��������


 ��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д� �����������Ż�ѧϰϵ�д�
�����������Ż�ѧϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ֽƬABC�У�AB=6��BC=8��AC=4���������µ�Ϳɫ���ֵ�����������ABC���Ƶ��ǣ�������
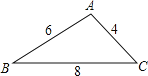
A. 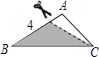 B.
B. 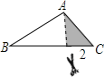 C.
C. 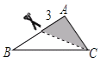 D.
D. 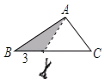
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ţ���������ǵ���Դ�أ�Ҳ����δ��֮�ǡ�����ʿ�㳡��ͣ��֮�أ��㳡�ϰ˴���¥��ˮ���������£������������Ϊ�����µĵر��Խ��������������������ʿ�㳡![]() ��¥��оͲ��
��¥��оͲ��![]() ��
��![]() ��
��![]() ����ɽṹ�ⶥ���߶�ˢ�������������ߣ�С��Ϊ�˲���
����ɽṹ�ⶥ���߶�ˢ�������������ߣ�С��Ϊ�˲���![]() �ĸ߶ȣ�������¥�ײ�
�ĸ߶ȣ�������¥�ײ�![]() �������ع㳡ǰ��
�������ع㳡ǰ��![]() ������
������![]() ���̶����¶�Ϊ
���̶����¶�Ϊ![]() ��б��������
��б��������![]() ������ͷ
������ͷ![]() ��Ȼ���ڸ����ϼ���ǰ��
��Ȼ���ڸ����ϼ���ǰ��![]() ����Ѳ��
����Ѳ��![]() ����
����![]() ��С���������˿�����������˿������������
��С���������˿�����������˿������������![]() �����Ϸ���
�����Ϸ���![]() ʱ�������ͷ
ʱ�������ͷ![]() �ĸ���Ϊ
�ĸ���Ϊ![]() ��¥��
��¥��![]() ������Ϊ
������Ϊ![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��ͬһƽ���ڣ���
��ͬһƽ���ڣ���![]() ��¥
��¥![]() �ĸ߶�ԼΪ���٣��������ȷ��
�ĸ߶�ԼΪ���٣��������ȷ��![]() �ף��ο����ݣ�
�ף��ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��
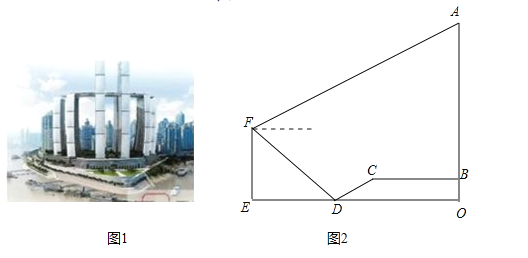
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ��
��![]() ��
��![]() ���ϵ����ߣ���
���ϵ����ߣ���![]() ������
������![]() ��.
��.
����:��ͼ�٣���![]() ��
��![]() ���ϣ�
���ϣ�![]() ��
��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ������
������![]() ��
��![]() ����
����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ����
����![]() ��ֵΪ .
��ֵΪ .
̽��:��ͼ�ڣ���![]() ��
��![]() ���ӳ����ϣ�
���ӳ����ϣ�![]() ��
��![]() ���ӳ��߽��ڵ�
���ӳ��߽��ڵ�![]() ��
�� ![]() ����
����![]() ��ֵ.
��ֵ.
Ӧ��:��̽���������£���![]() ��
��![]() ����
����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���ֽṹ�����Ŀ������ABC��ˮƽ����BC��18�ף�����AD��6�ף�����D��BC���е㣬��AD��BC��
��1����sinB��ֵ��
��2������Ҫ��װ֧��DE��EF�����е�E��AB�ϣ�BE��2AE����EF��BC������Ϊ��F����֧��DE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ�AD��Բ���У�������ͼ�У������̶ȵ�ֱ�߰�Ҫ��ͼ.
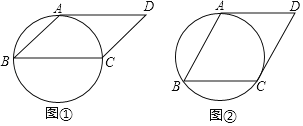
��1����BC��Բ��ֱ��������ƽ���ı���ABCD�ı�CD�ϵĸߣ�
��2����CD��Բ���У�����ƽ���ı���ABCD�ı�BC�ϵĸ�AE.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
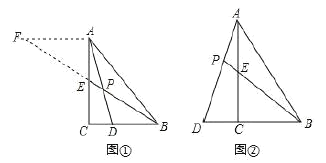
����Ŀ�����⣺��1����ͼ�٣���Rt��ABC�У�AB��AC��DΪBC����һ�㣨�����B��C�غϣ������߶�AD�Ƶ�A��ʱ����ת90��õ�AE������EC�����߶�BC��DC��EC֮������ĵ�����ϵʽΪ�� ����
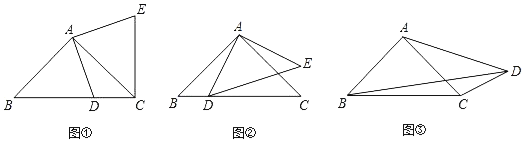
̽������2����ͼ�ڣ���Rt��ABC��Rt��ADE�У�AB��AC��AD��AE������ADE�Ƶ�A��ת��ʹ��D����BC���ϣ���̽���߶�AD��BD��CD֮������ĵ�����ϵ����֤����Ľ��ۣ�
Ӧ�ã���3����ͼ�ۣ����ı���ABCD�У���ABC����ACB����ADC��45�㣮��BD��9��CD��3����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ������4Ԫ/ǧ�˵ļ۸�һ��ˮ������������״�����ã��õ����ٴι���ͬһ��ˮ�����ڶ��ν����۸�ȵ�һ��ÿǧ�˱�����1Ԫ������ˮ������ǡ���ǵ�һ�ι���ˮ��������2����������ˮ�������ι���ˮ������ȥ��2000Ԫ��
��1����ˮ�������ηֱ����˶���Ԫ��ˮ����
��2���������У��������ν����ļ۸�ͬ����ˮ����������ͬ�ļ۸��۳�������һ�ι�����ˮ����3% ����ģ��ڶ��ι�����ˮ����4% ����ģ���ˮ����ϣ��������Щˮ������������3780Ԫ�����ˮ��ÿǧ���ۼ�����Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ţ�1����ͬѧΪ�˽�ijС����ͥ�¾���ˮ�������λ���֣�����������˸�С�����ּ�ͥ�������������ݽ�������������
�¾���ˮ�� | Ƶ�������� | Ƶ�� |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
25 | 2 | 0.04 |
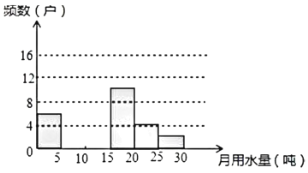
�����������⣺
��1���������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ����������
��2������С����1000����ͥ�����ݵ������ݹ��ƣ���С���¾���ˮ������20�ֵļ�ͥ��Լ�ж��ٻ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com