
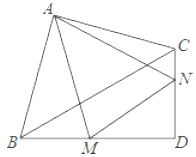
【题目】如图,在Rt△ABC和Rt△BCD中,∠BAC=∠BDC=90°,BC=4,AB=AC,∠CBD=30°,M,N分别在BD,CD上,∠MAN=45°,则△DMN的周长为_____.
【答案】2![]() +2
+2
【解析】
将△ACN绕点A逆时针旋转,得到△ABE,由旋转得出∠NAE=90°,AN=AE,∠ABE=∠ACD,∠EAB=∠CAN,求出∠EAM=∠MAN,根据SAS推出△AEM≌△ANM,根据全等得出MN=ME,求出MN=CN+BM,解直角三角形求出DC,即可求出△DMN的周长=BD+DC,代入求出答案即可.
将△ACN绕点A逆时针旋转,得到△ABE,如图:

由旋转得:∠NAE=90°,AN=AE,∠ABE=∠ACD,∠EAB=∠CAN,
∵∠BAC=∠D=90°,
∴∠ABD+∠ACD=360°﹣90°﹣90°=180°,
∴∠ABD+∠ABE=180°,
∴E,B,M三点共线,
∵∠MAN=45°,∠BAC=90°,
∴∠EAM=∠EAB+∠BAM=∠CAN+∠BAM=∠BAC﹣∠MAN=90°﹣45°=45°,
∴∠EAM=∠MAN,
在△AEM和△ANM中,
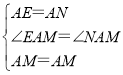 ,
,
∴△AEM≌△ANM(SAS),
∴MN=ME,
∴MN=CN+BM,
∵在Rt△BCD中,∠BDC=90°,∠CBD=30°,BC=4,
∴CD=![]() BC=2,BD=
BC=2,BD=![]() =2
=2![]() ,
,
∴△DMN的周长为DM+DN+MN=DM+DN+BM+CN=BD+DC=2![]() +2,
+2,
故答案为:2![]() +2.
+2.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一个质地均匀的转盘被分成3份,分别标有数字1、2、3,其中标有数字1、2的扇形的圆心角均为![]() .转动转盘,当它自动停止后,指针指向的数字即为转出的数字,此时称为转动转盘一次(指针指向两个扇形的分界线,则不计转动次数重新转动转盘,直到指针指向一个扇形的内部为止).
.转动转盘,当它自动停止后,指针指向的数字即为转出的数字,此时称为转动转盘一次(指针指向两个扇形的分界线,则不计转动次数重新转动转盘,直到指针指向一个扇形的内部为止).
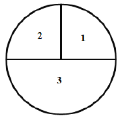
(1)转动转盘一次,求转出数字1的概率;
(2)转动转盘两次,用树状图或列表法求这两次转出数字之积等于9的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线 y=a![]() +bx+c 的对称轴为直线 x=2,与 x 轴的一个交点坐标为(4,0)其部分图象如图所示,下列结论其中结论正确的是( )
+bx+c 的对称轴为直线 x=2,与 x 轴的一个交点坐标为(4,0)其部分图象如图所示,下列结论其中结论正确的是( )
①抛物线过原点;②4a+b=0;③a﹣b+c<0;④抛物线线的顶点坐标为(2,b);⑤当 x<2 时,y 随 x 增大而增大
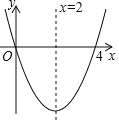
A.①②③B.③④⑤C.①②④D.①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+c与x轴交于A、B两点(A在B的左边),与y轴交于点C,抛物线上有一动点P
(1)若A(﹣2,0),C(0,﹣4)
①求抛物线的解析式;
②在①的情况下,若点P在第四象限运动,点D(0,﹣2),以BD、BP为邻边作平行四边形BDQP,求平行四边形BDQP面积的取值范围.
(2)若点P在第一象限运动,且a<0,连接AP、BP分别交y轴于点E、F,则问![]() 是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解初中学生每天在校体育活动的时间(单位:![]() ),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:
),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:
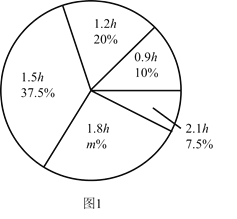
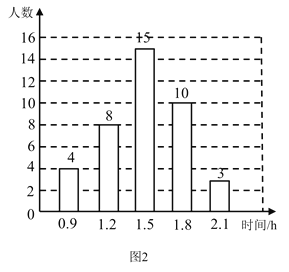
(Ⅰ)本次接受调查的初中学生人数为 ,图1中![]() 的值为 ;
的值为 ;
(Ⅱ)求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;
(Ⅲ)根据统计的这组每天在校体育活动时间的样本数据,若该校共有1200名初中学生,估计该校每天在校体育活动时间大于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
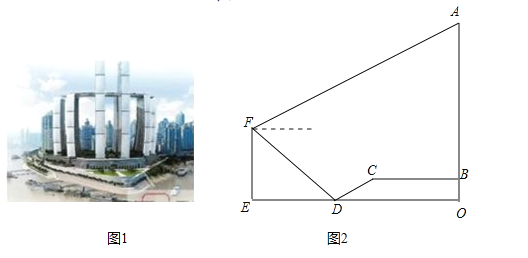
【题目】朝天门,既是重庆城的起源地,也是“未来之城”来福士广场的停泊之地,广场上八幢塔楼临水北向、错落有致,宛如轮扬帆起航,成为我市新的地标性建筑—“朝大杨帆”、来福士广场![]() 塔楼核芯筒于
塔楼核芯筒于![]() 年
年![]() 月
月![]() 日完成结构封顶,高度刷新了重庆的天际线,小明为了测量
日完成结构封顶,高度刷新了重庆的天际线,小明为了测量![]() 的高度,他从塔楼底部
的高度,他从塔楼底部![]() 出发,沿广场前进
出发,沿广场前进![]() 米至点
米至点![]() ,继而沿坡度为
,继而沿坡度为![]() 的斜坡向下走
的斜坡向下走![]() 米到达码头
米到达码头![]() ,然后在浮桥上继续前行
,然后在浮桥上继续前行![]() 米至巡船
米至巡船![]() ,在
,在![]() 处小明操作无人勘测机,当无人勘测机飞行至点
处小明操作无人勘测机,当无人勘测机飞行至点![]() 的正上方点
的正上方点![]() 时,测得码头
时,测得码头![]() 的俯角为
的俯角为![]() 、楼顶
、楼顶![]() 的仰角为
的仰角为![]() ,点
,点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 在同一平面内,则
在同一平面内,则![]() 塔楼
塔楼![]() 的高度约为多少?(结果精确到
的高度约为多少?(结果精确到![]() 米,参考数据:
米,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上的中线,点
边上的中线,点![]() 在射线
在射线![]() 上.
上.
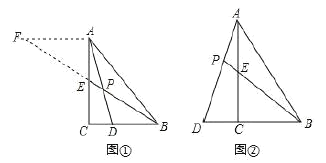
猜想:如图①,点![]() 在
在![]() 边上,
边上,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,则
,则![]() 的值为 .
的值为 .
探究:如图②,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,
, ![]() ,求
,求![]() 的值.
的值.
应用:在探究的条件下,若![]() ,
,![]() ,则
,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了1元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2000元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3% 的损耗,第二次购进的水果有4% 的损耗,该水果店希望售完这些水果获利不低于3780元,则该水果每千克售价至少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com