
【题目】已知:如图,![]() 中,
中,![]() .
.

(1)按要求作出图形:
①延长![]() 到点
到点![]() ,使
,使![]() ;②延长
;②延长![]() 到点
到点![]() ,使
,使![]() ;③连接
;③连接![]() ,
,![]() .
.
(2)猜想(1)中线段![]() 与
与![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
解:(1)完成作图
(2)![]() 与
与![]() 的大小关系是______
的大小关系是______
证明:
【答案】(1)作图见解析;(2)AD=BE,证明见解析.
【解析】
(1)根据题意画出图形;
(2)在AE上截取AF=AC,连结BF,证明△ABF≌△ABC,得到BF=BC,∠AFB=∠ACB,证明△ACD≌△EFB,根据全等三角形的性质证明即可.
解:(1)完成作图,如图所示,
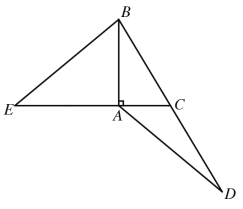
(2)![]() 与
与![]() 的大小关系是AD=BE
的大小关系是AD=BE
如下图所示,在AE上截取AF=AC,连结BF,
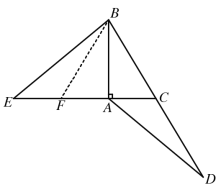
在△ABF和△ABC中,
∵AF=AC,∠FAB=∠CAB=90°,BA=BA,
∴△ABF≌△ABC(SAS),
∴BF=BC,∠AFB=∠ACB,
∴BF=CD,∠EFB=∠ACD,
在△ACD和△EFB中,
∵BF=CD,∠BFE=∠ACD,EF=AC,
∴△ACD≌△EFB(SAS),
∴AD=BE


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案科目:初中数学 来源: 题型:
【题目】下列四个命题:(1)三角形的一条中线把三角形分成面积相等的两部分;(2)有两边及其中一边的对角对应相等的两三角形全等;(3)点![]() 关于原点的对称点坐标为
关于原点的对称点坐标为![]() ;(4)若
;(4)若![]() ,则
,则![]() ;其中真命题的有 ( )
;其中真命题的有 ( )
A. (1)、(2)B. (1)、(3)C. (2)、(3)D. (3)、(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数![]() 的图象与
的图象与![]() 轴交于A、B两点(A点在B点左侧),顶点为
轴交于A、B两点(A点在B点左侧),顶点为![]() ,
,
(1)求A、B、![]() 三点坐标。
三点坐标。
(2)在平面直角坐标系中,用列表描点法,作出抛物线图象(如图),并根据图象回答,![]() 为何值时,函数值大于0?
为何值时,函数值大于0?
| |||||||
|
(3)将此抛物线向下平移2个单位,请写出平移后的解析式。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点![]() 是线段
是线段![]() 所在平面内任意一点,分别以
所在平面内任意一点,分别以![]() 、
、![]() 为边,在
为边,在![]() 同侧作等边
同侧作等边![]() 和等边
和等边![]() ,联结
,联结![]() 、
、![]() 交于点
交于点![]() .
.
(1)如图1,当点![]() 在线段
在线段![]() 上移动时,线段
上移动时,线段![]() 与
与![]() 的数量关系是:________;
的数量关系是:________;
(2)如图2,当点![]() 在直线
在直线![]() 外,且
外,且![]() ,仍分别以
,仍分别以![]() 、
、![]() 为边,在
为边,在![]() 同侧作等边
同侧作等边![]() 和等边
和等边![]() ,联结
,联结![]() 、
、![]() 交于点
交于点![]() .(1)的结论是否还存在?若成立,请证明;若不成立,请说明理由.此时
.(1)的结论是否还存在?若成立,请证明;若不成立,请说明理由.此时![]() 是否随
是否随![]() 的大小发生变化?若变化,写出变化规律,若不变,请求出
的大小发生变化?若变化,写出变化规律,若不变,请求出![]() 的度数;
的度数;
(3)如图3,在(2)的条件下,联结![]() ,求证:
,求证: ![]() 平分
平分![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年某市高中招生体育考试规定:九年级男生考试项目有A、B、C、D、E五类:其中A:1000米跑![]() 必考项目
必考项目![]() ;B:跳绳;C:引体向上;D:立定跳远;E:50米跑,再从B、C、D、E中各选两项进行考试.
;B:跳绳;C:引体向上;D:立定跳远;E:50米跑,再从B、C、D、E中各选两项进行考试.
![]() 若男生甲第一次选一项,直接写出男生甲选中项目E的概率.
若男生甲第一次选一项,直接写出男生甲选中项目E的概率.
![]() 若甲、乙两名九年级男生在选项的过程中,第一次都是选了项目E,那么他俩第二次同时选择跳绳或立定跳远的概率是多少?请用列表法或画树状图的方法加以说明并列出所有等可能的结果.
若甲、乙两名九年级男生在选项的过程中,第一次都是选了项目E,那么他俩第二次同时选择跳绳或立定跳远的概率是多少?请用列表法或画树状图的方法加以说明并列出所有等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
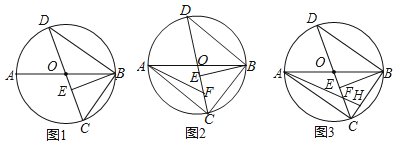
【题目】如图,AB、CD是![]() 的直径,
的直径,![]() 于E,连接BD.
于E,连接BD.
![]() 如图1,求证:
如图1,求证:![]() ;
;
![]() 如图2,F是OC上一点,
如图2,F是OC上一点,![]() ,求证:
,求证:![]() ;
;
![]() 在
在![]() 的条件下,连接BC,AF的延长线交BC于H,若
的条件下,连接BC,AF的延长线交BC于H,若![]() ,
,![]() ,求HF的长.
,求HF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)求C、D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足S△PCD=![]() S△BCD,求点P的坐标.
S△BCD,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com