
【题目】若二次函数![]() 的图象与
的图象与![]() 轴交于A、B两点(A点在B点左侧),顶点为
轴交于A、B两点(A点在B点左侧),顶点为![]() ,
,
(1)求A、B、![]() 三点坐标。
三点坐标。
(2)在平面直角坐标系中,用列表描点法,作出抛物线图象(如图),并根据图象回答,![]() 为何值时,函数值大于0?
为何值时,函数值大于0?
| |||||||
|
(3)将此抛物线向下平移2个单位,请写出平移后的解析式。
【答案】①A(3,0) B(1,0) P(2,1);②由图象可知,1<![]() <3时,函数值大于0;③
<3时,函数值大于0;③![]()
【解析】
(1)直接求出y=0时,x的值即可得出图象与x轴交点坐标,再利用配方法求出图象的顶点坐标即可;
(2)利用图象直接得出y<0时,即对应图象在x轴下方时,x的取值范围;
(3)利用二次函数平移的性质得出即可.
(1)∵y=x2+4x3与x轴交于A. B两点(A点在B点左侧),顶点为P,
∴0=x2+4x3,
解得:x1=1,x2=3,
∴A(1,0)、B(3,0),
![]()
∴P(2,1);
(2)
| -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| -8 | -3 | 0 | 1 | 0 | -3 | -8 |
如图所示:
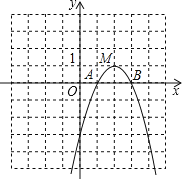
由图象可知,1<![]() <3时,函数值大于0;
<3时,函数值大于0;
(3)将此图象向下平移2个单位,
∴![]()


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
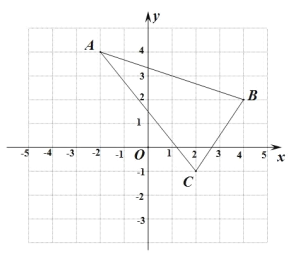
【题目】如图,△ABC 在平面直角坐标系中,点 A,B,C 的坐标分别为 A(-2,4),B(4,2),C(2,-1).
(Ⅰ)请在平面直角坐标系内,画出△ABC 关于 x 轴的对称图形△A1B1C1,其中,点 A,B,C 的对应点分别为A1,B1,C1;
(Ⅱ)请写出点C(2,-1)关于直线m(直线m上格点的横坐标都为-1)对称的点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
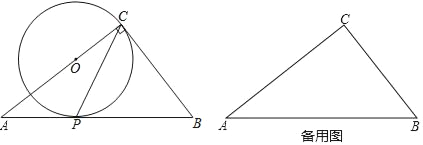
【题目】如图,在△ABC中,∠ACB=90°,经过点C的⊙O与斜边AB相切于点P,AC=8,BC=6.
(1)当点O在AC上时,求证:2∠ACP=∠B;
(2)在(1)的条件下,求⊙O的半径.
(3)若圆心O在△ABC之外,则CP的变化范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图像与正比例函数
的图像与正比例函数![]() 的图像都经过点
的图像都经过点![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 的图像上,点
的图像上,点![]() 在正比例函数
在正比例函数![]() 的图像上.
的图像上.
(1)求此正比例函数的解析式;
(2)求线段AB的长;
(3)求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列等式从左到右的变形中,属于因式分解的是( )
A.2x+1=x(2+![]() )
)
B.ax2﹣a=a(x2﹣1)
C.(x+2)(x﹣1)=x2+x﹣2
D.﹣4a2+9b2=(3b﹣2a)(3b+2a)
查看答案和解析>>
科目:初中数学 来源: 题型:
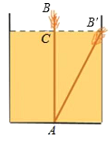
【题目】"引葭赴岸“是《九章算木》中的- -道題:”今有池一丈 ,葭生其中央,出水一尺,引葭赴岸,迺与岸芥.伺水深,葭氏各几何?"題意是:有一个边长为10尺的正方形池塘,一棵芦苇AB生长在它的中央,高出水面BC为1尺.如果把该芦苓沿与水池边垂直的方向拉向岸辺,那么芦革的顶部B恰好碰到岸边的B'. 向芦苇长多少? (画出几何图形并解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,![]() 中,
中,![]() .
.

(1)按要求作出图形:
①延长![]() 到点
到点![]() ,使
,使![]() ;②延长
;②延长![]() 到点
到点![]() ,使
,使![]() ;③连接
;③连接![]() ,
,![]() .
.
(2)猜想(1)中线段![]() 与
与![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
解:(1)完成作图
(2)![]() 与
与![]() 的大小关系是______
的大小关系是______
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数![]() 、
、![]() 、
、![]() 都是常数,且
都是常数,且![]() 叫做“奇特函数”,当
叫做“奇特函数”,当![]() 时,奇特函数
时,奇特函数![]() 就成为反比例函数
就成为反比例函数![]() 是常数,且
是常数,且![]() .
.
![]() 若矩形的两边长分别是
若矩形的两边长分别是![]() 、
、![]() ,当两边长分别增加
,当两边长分别增加![]() 、
、![]() 后得到的新矩形的面积是
后得到的新矩形的面积是![]() ,求
,求![]() 与
与![]() 的函数关系式,并判断这个函数是否“奇特函数”;
的函数关系式,并判断这个函数是否“奇特函数”;
![]() 如图在直角坐标系中,点
如图在直角坐标系中,点![]() 为原点矩形
为原点矩形![]() 的顶点,
的顶点,![]() 、
、![]() 坐标分别为
坐标分别为![]() 、
、![]() ,点
,点![]() 是
是![]() 中点,连接
中点,连接![]() 、
、![]() 交于
交于![]() ,“奇特函数”
,“奇特函数”![]() 的图象经过点
的图象经过点![]() 、
、![]() ,求这个函数的解析式,并判断
,求这个函数的解析式,并判断![]() 、
、![]() 、
、![]() 三点是否在这个函数图象上;
三点是否在这个函数图象上;
![]() 对于
对于![]() 中的“奇特函数”
中的“奇特函数”![]() 的图象,能否经过适当的变换后与一个反比例函数图象重合,若能,请直接写出具体的变换过程和这个反比例函数解析式;若不能,请简述理由.
的图象,能否经过适当的变换后与一个反比例函数图象重合,若能,请直接写出具体的变换过程和这个反比例函数解析式;若不能,请简述理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+ax+a-2=0.
(1)求证:不论a取何实数,该方程都有两个不相等的实数根;
(2)若该方程的一个根为1,求a的值及该方程的另一根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com