练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

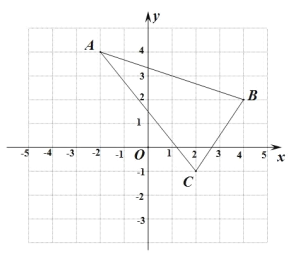
    【题目】如图，△ABC 在平面直角坐标系中，点 A，B，C 的坐标分别为 A（-2,4），B（4,2），C（2，-1）.

    （Ⅰ）请在平面直角坐标系内，画出△ABC 关于 x 轴的对称图形△A1B1C1，其中，点 A，B，C 的对应点分别为A1，B1，C1；

    （Ⅱ）请写出点C（2，-1）关于直线m（直线m上格点的横坐标都为-1）对称的点C2的坐标.

    【答案】（Ⅰ）见解析；（Ⅱ）C2的坐标为：（-4，-1）.

    【解析】

    （Ⅰ）根据关于x轴对称的点的坐标特点画出△A1B1C1即可；

    （Ⅱ）在平面直角坐标系中画出点C2即可写出点C2的坐标.

    （Ⅰ）如图所示，△A1B1C1即为所画；

    （Ⅱ）画出点C2，如上图可得出点C2的坐标为：（-4，-1）.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】课题学习：设计概率模拟实验．

    在学习概率时，老师说：“掷一枚质地均匀的硬币，大量重复实验后，正面朝上的概率约是．”小海、小东、小英分别设计了下列三个模拟实验：

    小海找来一个啤酒瓶盖（如图1）进行大量重复抛掷，然后计算瓶盖口朝上的次数与总次数的比值；

    小东用硬纸片做了一个圆形转盘，转盘上分成8个大小一样的扇形区域，并依次标上1至8个数字（如图2），转动转盘10次，然后计算指针落在奇数区域的次数与总次数的比值；

    小英在一个不透明的盒子里放了四枚除颜色外都相同的围棋子（如图3），其中有三枚是白子，一枚是黑子，从中随机同时摸出两枚棋子，并大量重复上述实验，然后计算摸出的两枚棋子颜色不同的次数与总次数的比值．

    根据以上材料回答问题：

    小海、小东、小英三人中，哪一位同学的实验设计比较合理，并简要说出其他两位同学实验的不足之处．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,直线AB分别与两坐标轴交于点A（4,0）.B（0,8）,点C的坐标为（2,0）.

    （1）求直线AB的解析式；

    （2）在线段AB上有一动点P.

    ①过点P分别作x,y轴的垂线,垂足分别为点E,F,若矩形OEPF的面积为6,求点P的坐标.

    ②连结CP,是否存在点P,使与相似,若存在,求出点P的坐标,若不存在,请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB∥CD，EF交AB于E，交CD于F，EP平分∠AEF，FP平分∠CFE，直线MN经过点P并与AB，CD分别交于点M，N.

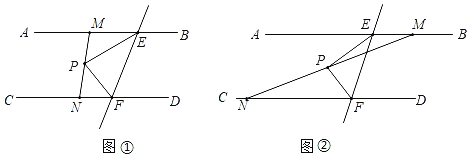
    (1)如图①，求证：EM+FN＝EF；

    (2)如图②，(1)的结论是否成立？若成立，请证明；若不成立，直接写出EM，FN，EF三条线段的数量关系.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=kx+b（k≠0）与抛物线y=ax2（a≠0）交于A，B两点，且点A的横坐标是-2，点B的横坐标是3，则以下结论：

    ①抛物线y=ax2（a≠0）的图象的顶点一定是原点；

    ②x＞0时，直线y=kx+b（k≠0）与抛物线y=ax2（a≠0）的函数值都随着x的增大而增大；

    ③AB的长度可以等于5；

    ④△OAB有可能成为等边三角形；

    ⑤当-3＜x＜2时，ax2+kx＜b，

    其中正确的结论是（ ）

    A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列关于概率的说法，错误的是（ ）

    A. 明天下雨的概率是80%，即明天80%的时间都下雨；

    B. 做投掷硬币试验时，投掷的次数足够多时，正面朝上的频率就越接近于；

    C. “13人中至少有2人生肖相同”，这是一个必然事件。

    D. 连掷两枚骰子，它们的点数相同的概率是；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】E、F分别是边长为4的菱形ABCD中边BC、CD上的点，∠B=∠EAF=60°，△AEF的周长为，则的最小值是_______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，E是AB的中点，连接DE、CE．

    （1）求证：△ADE≌△BCE；

    （2）若AB=6，AD=4，求△CDE的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若二次函数的图象与轴交于A、B两点（A点在B点左侧），顶点为，

    （1）求A、B、三点坐标。

    （2）在平面直角坐标系中，用列表描点法，作出抛物线图象（如图），并根据图象回答，为何值时，函数值大于0？

    （3）将此抛物线向下平移2个单位，请写出平移后的解析式。

    查看答案和解析>>

    同步练习册答案