
【题目】如图已知在![]() 中,
中,![]() ,
,![]() ,直角
,直角![]() 的顶点
的顶点![]() 是
是![]() 的中点,两边
的中点,两边![]() 、
、![]() 分别交
分别交![]() 和
和![]() 于点
于点![]() 、
、![]() ,给出以下五个结论正确的个数有( )
,给出以下五个结论正确的个数有( )
①![]() ;②
;②![]() ;③
;③![]() ≌
≌![]() ;④
;④![]() 是等腰直角三角形;⑤当
是等腰直角三角形;⑤当![]() 在
在![]() 内绕顶点
内绕顶点![]() 旋转时(点
旋转时(点![]() 不与
不与![]() 、
、![]() 重合),
重合),![]() .
.

A.2B.3C.4D.5
【答案】D
【解析】
根据等腰直角三角形的性质可得AP⊥BC,AP=PC,∠EAP=∠C=45°,根据同角的余角相等求出∠APE=∠CPF,判定②正确,然后利用“角边角”证明△APE和△CPF全等,根据全等三角形的可得AE=CF,判定①正确,再根据等腰直角三角形的定义得到△EFP是等腰直角三角形,判定④正确;根据全等三角形的判定判断③正确;根据全等三角形的面积相等可得△APE的面积等于△CPF的面积相等,然后求出四边形AEPF的面积等于△ABC的面积的一半,判定⑤正确.
解:∵AB=AC,∠BAC=90°,点P是BC的中点,
∴AP⊥BC,AP=PC,∠EAP=∠C=45°,
∴∠APF+∠CPF=90°,
∵∠EPF是直角,
∴∠APF+∠APE=90°,
∴∠APE=∠CPF,故②正确;
在△APE和△CPF中,
 ,
,
∴△APE≌△CPF(ASA),
∴AE=CF,故①正确;
∵△AEP≌△CFP,同理可证△APF≌△BPE,故③正确;
∴△EFP是等腰直角三角形,故④正确;
∵△APE≌△CPF,
∴S△APE=S△CPF,
∴S四边形AEPF=S△AEP+S△APF=S△CPF+S△BPE=![]() S△ABC.,故⑤正确,
S△ABC.,故⑤正确,
综上所述,正确的结论有①②③④⑤共5个.
故选择:D.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定:抛物线![]() 的伴随直线为
的伴随直线为![]() .例如:抛物线
.例如:抛物线![]() 的伴随直线为
的伴随直线为![]() ,即y=2x﹣1.
,即y=2x﹣1.
(1)在上面规定下,抛物线![]() 的顶点坐标为 ,伴随直线为 ,抛物线
的顶点坐标为 ,伴随直线为 ,抛物线![]() 与其伴随直线的交点坐标为 和 ;
与其伴随直线的交点坐标为 和 ;
(2)如图,顶点在第一象限的抛物线![]() 与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
①若∠CAB=90°,求m的值;

②如果点P(x,y)是直线BC上方抛物线上的一个动点,△PBC的面积记为S,当S取得最大值![]() 时,求m的值.
时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种成本为40元![]() 千克的商品,若按50元
千克的商品,若按50元![]() 千克销售,一个月可售出500千克,现打算涨价销售,据市场调查,涨价x元时,月销售量为m千克,m是x的一次函数,部分数据如下表:
千克销售,一个月可售出500千克,现打算涨价销售,据市场调查,涨价x元时,月销售量为m千克,m是x的一次函数,部分数据如下表:

![]() 观察表中数据,直接写出m与x的函数关系式:_______________:当涨价5元时,计算可得月销售利润是___________元;
观察表中数据,直接写出m与x的函数关系式:_______________:当涨价5元时,计算可得月销售利润是___________元;
![]() 当售价定多少元时,会获得月销售最大利润,求出最大利润.
当售价定多少元时,会获得月销售最大利润,求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生对毒品危害性的认识,我市相关部门每个月都要对学生进行“禁毒知识应知应会”测评.为了激发学生的积极性,某校对达到一定成绩的学生授予“禁毒小卫士”的荣誉称号.为了确定一个适当的奖励目标,该校随机选取了七年级20名学生在5月份测评的成绩.数据如下:
收集数据:90 91 89 96 90 98 90 97 91 98 99 97 91 88 90 97 95 90 95 88
整理、描述数据:
成绩/分 | 88 | 89 | 90 | 91 | 95 | 96 | 97 | 98 | 99 |
学生人数 | 2 | 1 |
| 3 | 2 | 1 |
| 2 | 1 |
数据样本数据的平均数、众数和中位数如下表
平均数 | 众数 | 中位数 |
93 |
|
|
应用数据
(1)由上表填空:![]() ________,
________,![]() ________,
________,![]() ________,
________,![]() ________,
________,
(2)根据所给数据,如果该校想确定七年级前![]() 的学生为“良好”等次,你认为“良好”等次的测评成绩至少定为________分.
的学生为“良好”等次,你认为“良好”等次的测评成绩至少定为________分.
(3)根据数据分析,该校决定在七年级授予测评成绩前![]() 的学生“禁毒小卫士”荣誉称号.请估计评选该荣誉称号的最低分数,并说明理由.
的学生“禁毒小卫士”荣誉称号.请估计评选该荣誉称号的最低分数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他各项费用80元.
销售单价x(元) | 3.5 | 5.5 |
销售量y(袋) | 280 | 120 |
(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边三角形ABC的边长为2,DE是它的中位线,则下面五个结论:①.DE=1②.△CDE∽△CAB ③△CDE 的面积与四边形ABED的面积之比为1:3 ④梯形ABED的中位线长为![]() ⑤. DG:GB=1:2 ,其中正确的有( )
⑤. DG:GB=1:2 ,其中正确的有( )

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m22=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1x2)2+m2=21,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() .
.
(1)证明该方程一定有两个不相等的实数根;
(2)设该方程两根为x1、x2(x1<x2).
①当![]() 时,试确定y值的范围;
时,试确定y值的范围;
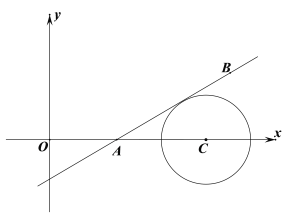
②如图,平面直角坐标系中有三点A、B、C,坐标分别为(x1,0)、(x2,3)、(7,0).以点C为圆心,2个单位长度为半径的圆与直线AB相切,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com