
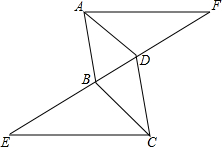
 如图所示,△ADF≌△CBE,且点E,B,D,F在一条直线上,判断AD与BC的位置关系,并说明理由.
如图所示,△ADF≌△CBE,且点E,B,D,F在一条直线上,判断AD与BC的位置关系,并说明理由.  一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:解答题
 如图所示是某养殖专业户建立的一个矩形场地,一边靠墙,另三边除大门外用篱笆围成.已知篱笆总长为30m,门宽是2m,若设这块场地的宽为xm.
如图所示是某养殖专业户建立的一个矩形场地,一边靠墙,另三边除大门外用篱笆围成.已知篱笆总长为30m,门宽是2m,若设这块场地的宽为xm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+1)(1+a) | B. | ($\frac{1}{2}$a+b)(b-$\frac{1}{2}$a) | C. | (-x+y)(x-y) | D. | (x2-y)(x+y2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com