
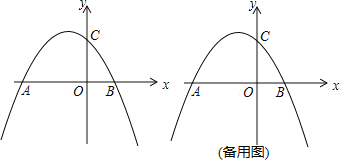
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点A、B,与y轴交于点C,点A的坐标为(-4,0),P是抛物线上一点 (点P与点A、B、C不重合).
轴交于点A、B,与y轴交于点C,点A的坐标为(-4,0),P是抛物线上一点 (点P与点A、B、C不重合).
(1)b= ,点B的坐标是 ;
(2)设直线PB直线AC交于点M,是否存在这样的点P,使得PM:MB=1:2?若存在,求出点P的横坐标;若不存在,请说明理由;
(3)连接AC、BC,判断∠CAB和∠CBA的数量关系,并说明理由.
【答案】(1)![]() ;(
;(![]() ,0);(2)存在点P的横坐标为
,0);(2)存在点P的横坐标为![]() 或
或![]() .(3)∠CBA=2∠CAB.理由见解析.
.(3)∠CBA=2∠CAB.理由见解析.
【解析】
(1)由点A的坐标,利用二次函数图象上点的坐标特征可求出b的值,代入y=0求出x值,进而可得出点B的坐标;
(2)(解法一)代入x=0求出y值,进而可得出点C的坐标,由点A、C的坐标利用待定系数法可求出直线AC的解析式,假设存在,设点M的坐标为(m,![]() m+2),分B、P在直线AC的同侧和异侧两种情况考虑,由点B、M的坐标结合PM:MB=1:2即可得出点P的坐标,再利用二次函数图象上点的坐标特征可得出关于m的一元二次方程,解之即可得出结论;
m+2),分B、P在直线AC的同侧和异侧两种情况考虑,由点B、M的坐标结合PM:MB=1:2即可得出点P的坐标,再利用二次函数图象上点的坐标特征可得出关于m的一元二次方程,解之即可得出结论;
(解法二)代入x=0求出y值,进而可得出点C的坐标,由点A、C的坐标利用待定系数法可求出直线AC的解析式,过点B作BB′∥y轴交直线AC于点B′,过点P作PP′∥y轴交直线AC于点P′,由点B的坐标可得出BB′的值,结合相似三角形的性质可得出PP′的值,设点P的坐标为(x,-![]() x2-
x2-![]() x+2),则点P′的坐标为(x,
x+2),则点P′的坐标为(x,![]() x+2),结合PP′的值可得出关于x的含绝对值符号的一元二次方程,解之即可得出结论;
x+2),结合PP′的值可得出关于x的含绝对值符号的一元二次方程,解之即可得出结论;
(3)作∠CBA的角平分线,交y轴于点E,过点E作EF⊥BC于点F,设OE=n,则CE=2-n,EF=n,利用面积法可求出n值,进而可得出![]() ,结合∠AOC=90°=∠BOE可证出△AOC∽△BOE,根据相似三角形的性质可得出∠CAO=∠EBO,再根据角平分线的性质可得出∠CBA=2∠EBO=2∠CAB,此题得解.
,结合∠AOC=90°=∠BOE可证出△AOC∽△BOE,根据相似三角形的性质可得出∠CAO=∠EBO,再根据角平分线的性质可得出∠CBA=2∠EBO=2∠CAB,此题得解.
(1)![]() 点
点![]() 在二次函数
在二次函数![]() 的图象上,
的图象上,
![]() ,
,
![]() .
.
当![]() 时, 有
时, 有![]() ,
,
解得:![]() ,
,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
故答案为:![]() ;
;![]() ,
,![]() .
.
(2) (方 法一) 当![]() 时,
时,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() 、
、![]() 代入
代入![]() 中,
中,
得:![]() ,解得:
,解得:![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
假设存在, 设点![]() 的坐标为
的坐标为![]() .
.
①当点![]() 、
、![]() 在直线
在直线![]() 的异侧时, 点
的异侧时, 点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,
![]() 点
点![]() 在抛物线
在抛物线![]() 上,
上,
![]()
![]() ,
,
整理, 得:![]() .
.
![]() △
△![]() ,
,
![]() 方程无解, 即不存在符合题意得点
方程无解, 即不存在符合题意得点![]() ;
;
②当点![]() 、
、![]() 在直线
在直线![]() 的同侧时, 点
的同侧时, 点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,
![]() 点
点![]() 在抛物线
在抛物线![]() 上,
上,
![]()
![]() ,
,
整理, 得:![]() ,
,
解得:![]() ,
,![]() ,
,
![]() 点
点![]() 的横坐标为
的横坐标为![]() 或
或![]() .
.
综上所述: 存在点![]() ,使得
,使得![]() ,点
,点![]() 的横坐标为
的横坐标为![]() 或
或![]() .
.
(3)![]() ,理由如下:
,理由如下:
作![]() 的角平分线, 交
的角平分线, 交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,如图 2 所示 .
,如图 2 所示 .
![]() 点
点![]() ,
,![]() ,点
,点![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,
由面积法, 可知:![]() ,即
,即![]() ,
,
解得:![]() .
.
![]()
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )

A. AB=24m B. MN∥AB
C. △CMN∽△CAB D. CM:MA=1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
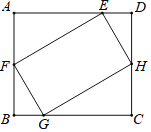
【题目】如图,矩形EFGH的四个顶点分别在矩形ABCD的各条边上,AB=EF,FG=2,GC=3.有以下四个结论:①∠BGF=∠CHG;②△BFG≌△DHE;③tan∠BFG=![]() ;④矩形EFGH的面积是4
;④矩形EFGH的面积是4![]() .其中一定成立的是______.(把所有正确结论的序号填在横线上)
.其中一定成立的是______.(把所有正确结论的序号填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小学学生较多,为了便于学生尽快就餐,师生约定:早餐一人一份,一份两样,一样一个,食堂师傅在窗口随机发放(发放的食品价格一样),食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品.
(1)按约定,“小李同学在该天早餐得到两个油饼”是 事件;(可能,必然,不可能)
(2)请用列表或树状图的方法,求出小张同学该天早餐刚好得到猪肉包和油饼的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象C经过(-5,0),![]() ,(1,6)三点,直线l的解析式为y=2x-3.
,(1,6)三点,直线l的解析式为y=2x-3.
(1)求抛物线C的解析式;
(2)判断抛物线C与直线l有无交点;
(3)若与直线l平行的直线y=2x+m与抛物线C只有一个公共点P,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,弦AB,CD相交于点E,
中,弦AB,CD相交于点E,![]() =
=![]() ,点D在
,点D在![]() 上,连结CO,并延长CO交线段AB于点F,连接OA,OB,且OA=2,∠OBA=30°
上,连结CO,并延长CO交线段AB于点F,连接OA,OB,且OA=2,∠OBA=30°
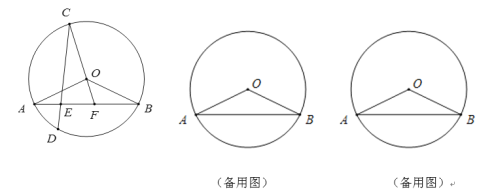
(1)求证:∠OBA=∠OCD;
(2)当![]() AOF是直角三角形时,求EF的长;
AOF是直角三角形时,求EF的长;
(3)是否存在点F,使得![]() ,若存在,请求出EF的长,若不存在,请说明理由.
,若存在,请求出EF的长,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG∥CD交BE于点G,连接CG.
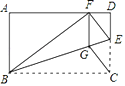
(1)求证:四边形CEFG是菱形;
(2)若AB=6,AD=10,求四边形CEFG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
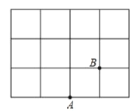
【题目】如图,在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,任意三个格点组成的三角形面积如果不小于1则称为“离心三角形”,而如果面积恰好等于1则称为“环绕三角形”.![]() 是网格图形中已知的两个格点,点
是网格图形中已知的两个格点,点![]() 是另一个格点,且满足
是另一个格点,且满足![]() 是“离心三角形”,则
是“离心三角形”,则![]() 是“环绕三角形”的概率是__________.
是“环绕三角形”的概率是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地进行中考体育测试,规定测试项目分为必选项目与自选项目,男生自选项目是50米跑(A)、立定跳远(B)、引体向上(C)、1分钟跳绳(D),每个男生要在四个项目抽选两项进行测试.测试前,每个学生先抽一个,确定一个,再在所剩三个项目中再抽一个.张强同学的这四个项目中,他自认为50米跑更擅长.
(1)若张强先抽到立定跳远,然后再从剩下的项目中随机选择一项参加测试,则他刚好选中50米跑的概率是_______.
(2)若张强连续随机抽取两项,求其中抽中50米跑的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com