
【题目】某地进行中考体育测试,规定测试项目分为必选项目与自选项目,男生自选项目是50米跑(A)、立定跳远(B)、引体向上(C)、1分钟跳绳(D),每个男生要在四个项目抽选两项进行测试.测试前,每个学生先抽一个,确定一个,再在所剩三个项目中再抽一个.张强同学的这四个项目中,他自认为50米跑更擅长.
(1)若张强先抽到立定跳远,然后再从剩下的项目中随机选择一项参加测试,则他刚好选中50米跑的概率是_______.
(2)若张强连续随机抽取两项,求其中抽中50米跑的概率.
 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
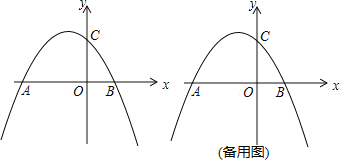
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点A、B,与y轴交于点C,点A的坐标为(-4,0),P是抛物线上一点 (点P与点A、B、C不重合).
轴交于点A、B,与y轴交于点C,点A的坐标为(-4,0),P是抛物线上一点 (点P与点A、B、C不重合).
(1)b= ,点B的坐标是 ;
(2)设直线PB直线AC交于点M,是否存在这样的点P,使得PM:MB=1:2?若存在,求出点P的横坐标;若不存在,请说明理由;
(3)连接AC、BC,判断∠CAB和∠CBA的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:顶点、开口大小相同,开口方向相反的两个二次函数互为“反簇二次函数”.
(1)已知二次函数y=﹣(x﹣2)2+3,则它的“反簇二次函数”是__________________;
(2)已知关于x的二次函数y1=2x2﹣2mx+m+1和y2=ax2+bx+c,其中y1的图像经过点(1,1).若y1+y2与y1互为“反簇二次函数”.求函数y2的表达式,并直接写出当0≤x≤3时,y2的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为△ABC的内心,过点E作MN∥BC交AB于点M,交AC于点N,若AB=7,AC=5,BC=6,则MN的长为( )

A. 3.5B. 4C. 5D. 5.5
查看答案和解析>>
科目:初中数学 来源: 题型:
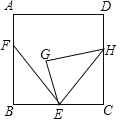
【题目】如图,正方形 ABCD 中,点 E,F 分别在 BC 和 AB 上,BE=3,AF=2,BF=4,将△ BEF 绕点 E 顺时针旋转,得到△GEH,当点 H 落在 CD 边上时,F,H 两点之间的距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师要求学生探究如下问题:
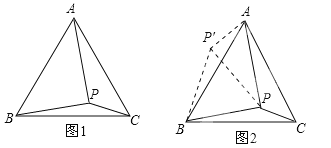
(1)如图1,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,试求∠BPC的度数.李华同学一时没有思路,当他认真分析题目信息后,发现以PA、PB、PC的长为边构成的三角形是直角三角形,他突然有了正确的思路:如图2,将△BPC绕点B逆时针旋转60°,得到△BP′A,连接PP′,易得△P′PB是等边三角形,△PP′A是直角三角形.则∠BPC=_______°.
,PC=1,试求∠BPC的度数.李华同学一时没有思路,当他认真分析题目信息后,发现以PA、PB、PC的长为边构成的三角形是直角三角形,他突然有了正确的思路:如图2,将△BPC绕点B逆时针旋转60°,得到△BP′A,连接PP′,易得△P′PB是等边三角形,△PP′A是直角三角形.则∠BPC=_______°.
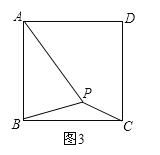
(2)如图3,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1,试求∠BPC的度数.
,PC=1,试求∠BPC的度数.
(3)在图3中,若在正方形ABCD内有另一点Q,QA=a,QB=b,QC=c(a>b,a>c),试猜想a,b,c满足什么条件时,∠BQC的度数与第(2)问中∠BPC的度数相等,请直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在Rt△ABC中,∠C=90°,点O在边BC上,以点O为圆心,OB为半径的圆经过点A,过点A作直线AD,使∠CAD=2∠B.

(1)判断直线AD与⊙O的位置关系,并说明理由;
(2)若OB=4,∠CAD=60°,请直接写出图中弦AB与![]() 围成的阴影部分的面积.
围成的阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
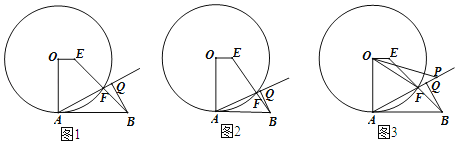
【题目】如图,OA是⊙O的半径,点E为圆内一点,且OA⊥OE,AB是⊙O的切线,EB交⊙O于点F,BQ⊥AF于点Q.
(1)如图1,求证:OE∥AB;
(2)如图2,若AB=AO,求![]() 的值;
的值;
(3)如图3,连接OF,∠EOF的平分线交射线AF于点P,若OA=2,cos∠PAB=![]() ,求OP的长.
,求OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
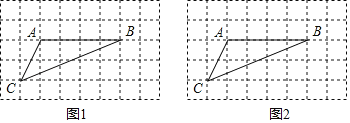
【题目】如图,在8×5的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在小正方形的顶点上.
(1)在图1中画出△ABD(点D在小正方形的顶点上),使△ABD的周长等于△ABC的周长,且四边形ACBD是中心对称图形;
(2)在图2中找一点E(点E在小正方形的顶点上),使tan∠AEB=2(AE<EB),且四边形ACEB的对边不平行,并直接写出图2中四边形ACEB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com