
ЁОЬтФПЁПдкЪ§бЇПЮЩЯЃЌРЯЪІвЊЧѓбЇЩњЬНОПШчЯТЮЪЬтЃК
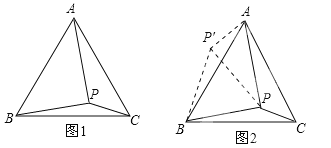
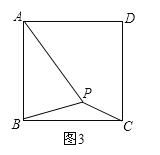
(1)ШчЭМ1ЃЌдкЕШБпШ§НЧаЮABCФкгавЛЕуPЃЌЧвPA=2ЃЌPB=![]() ЃЌPC=1ЃЌЪдЧѓЁЯBPCЕФЖШЪ§.РюЛЊЭЌбЇвЛЪБУЛгаЫМТЗЃЌЕБЫћШЯецЗжЮіЬтФПаХЯЂКѓЃЌЗЂЯжвдPAЁЂPBЁЂPCЕФГЄЮЊБпЙЙГЩЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃЌЫћЭЛШЛгаСЫе§ШЗЕФЫМТЗЃКШчЭМ2ЃЌНЋЁїBPCШЦЕуBФцЪБеыа§зЊ60ЁуЃЌЕУЕНЁїBPЁфAЃЌСЌНгPPЁфЃЌвзЕУЁїPЁфPBЪЧЕШБпШ§НЧаЮЃЌЁїPPЁфAЪЧжБНЧШ§НЧаЮ.дђЁЯBPC=_______Ёу.
ЃЌPC=1ЃЌЪдЧѓЁЯBPCЕФЖШЪ§.РюЛЊЭЌбЇвЛЪБУЛгаЫМТЗЃЌЕБЫћШЯецЗжЮіЬтФПаХЯЂКѓЃЌЗЂЯжвдPAЁЂPBЁЂPCЕФГЄЮЊБпЙЙГЩЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃЌЫћЭЛШЛгаСЫе§ШЗЕФЫМТЗЃКШчЭМ2ЃЌНЋЁїBPCШЦЕуBФцЪБеыа§зЊ60ЁуЃЌЕУЕНЁїBPЁфAЃЌСЌНгPPЁфЃЌвзЕУЁїPЁфPBЪЧЕШБпШ§НЧаЮЃЌЁїPPЁфAЪЧжБНЧШ§НЧаЮ.дђЁЯBPC=_______Ёу.
(2)ШчЭМ3ЃЌдке§ЗНаЮABCDФкгавЛЕуPЃЌЧвPA=![]() ЃЌBP=
ЃЌBP=![]() ЃЌPC=1ЃЌЪдЧѓЁЯBPCЕФЖШЪ§.
ЃЌPC=1ЃЌЪдЧѓЁЯBPCЕФЖШЪ§.
(3)дкЭМ3жаЃЌШєдке§ЗНаЮABCDФкгаСэвЛЕуQЃЌQA=aЃЌQB=bЃЌQC=c(a>bЃЌa>c)ЃЌЪдВТЯыaЃЌbЃЌcТњзуЪВУДЬѕМўЪБЃЌЁЯBQCЕФЖШЪ§гыЕк(2)ЮЪжаЁЯBPCЕФЖШЪ§ЯрЕШЃЌЧыжБНгаДГіНсТл.
ЁОД№АИЁПЃЈ1ЃЉ150ЁуЃЛЃЈ2ЃЉЁЯBPCЃН135ЁуЃЛЃЈ3ЃЉa2ЃНc2+2b2ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтвзжЄЕУЁїPЁфPBЪЧе§Ш§НЧаЮЃЌЁїPЁфPAЪЧжБНЧШ§НЧаЮЃЌНјЖјПЩЕУЁЯBP'PгыЁЯAP'PЕФЖШЪ§ЃЌдйИљОна§зЊЕФаджЪМДЕУНсЙћЃЛ
ЃЈ2ЃЉЗТееЃЈ1ЃЉЕФЫМТЗЃЌНЋЁїBPCШЦЕуBФцЪБеыа§зЊ90ЁуЃЌЕУЕНЁїBP'AЃЌШЛКѓСЌНгPP'ЃЌИљОна§зЊЕФаджЪПЩЕУЁї![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌИљОнЙДЙЩЖЈРэЕФФцЖЈРэПЩЕУЁЯAP'PЃН90ЁуЃЌДгЖјПЩЕУНсТлЃЛ
ЪЧЕШбќжБНЧШ§НЧаЮЃЌИљОнЙДЙЩЖЈРэЕФФцЖЈРэПЩЕУЁЯAP'PЃН90ЁуЃЌДгЖјПЩЕУНсТлЃЛ
ЃЈ3ЃЉЗТееЃЈ2ЃЉЕФЫМТЗЃЌНЋЁїBQCШЦЕуBФцЪБеыа§зЊ90ЁуЃЌЕУЕНЁїBQ'AЃЌШЛКѓСЌНгQQ'ЃЌИљОна§зЊЕФаджЪПЩЕУЁї![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌНјвЛВНМДЕУЁЯAQ'QЃН90ЁуЃЌШЛКѓИљОнЙДЙЩЖЈРэМДПЩЕУГіНсТлЃЎ
ЪЧЕШбќжБНЧШ§НЧаЮЃЌНјвЛВНМДЕУЁЯAQ'QЃН90ЁуЃЌШЛКѓИљОнЙДЙЩЖЈРэМДПЩЕУГіНсТлЃЎ
НтЃКЃЈ1ЃЉЁпНЋЁїBPCШЦЕуBФцЪБеыа§зЊ60ЁуЃЌЕУЕНЁїBPЁфAЃЌ
ЁрBP= BPЁфЃЌЁЯPBP'ЃН60ЁуЃЌ
ЁрЁїPЁфPBЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯBP'PЃН60ЁуЃЌ
ЁпPA=2ЃЌPP'= BP=![]() ЃЌPC=PЁфA=1ЃЌ
ЃЌPC=PЁфA=1ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЁїPЁфPAЪЧжБНЧШ§НЧаЮЃЌЁЯAP'PЃН90ЁуЃЌ
ЁрЁЯAP'BЃН150ЁуЃЌ
ЁрЁЯBPCЃНЁЯAP'BЃН150ЁуЃЛ
ЙЪД№АИЮЊЃК150ЁуЃЛ
ЃЈ2ЃЉШчЭМ4ЃЌНЋЁїBPCШЦЕуBФцЪБеыа§зЊ90ЁуЃЌЕУЕНЁїBP'AЃЌСЌНгPP'ЃЌ
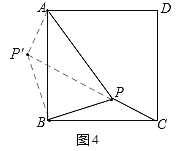
ЁрBPЃНBP'ЃН![]() ЃЌЁЯPBP'ЃН90ЁуЃЌPCЃНP'AЃЌЁЯAP'BЃНЁЯBPCЃЌ
ЃЌЁЯPBP'ЃН90ЁуЃЌPCЃНP'AЃЌЁЯAP'BЃНЁЯBPCЃЌ
ЁрЁЯBP'PЃН45ЁуЃЌPP'ЃН![]() ЃН2ЃЌ
ЃН2ЃЌ
ЁпP'P2+P'A2ЃН5ЃЌPA2ЃН5ЃЌ
ЁрP'P2+P'A2ЃНPA2ЃЌ
ЁрЁЯAP'PЃН90ЁуЃЌ
ЁрЁЯAP'BЃНЁЯAP'P+ЁЯBP'PЃН135ЁуЃЌ
ЁпЁЯAP'BЃНЁЯBPCЃЌ
ЁрЁЯBPCЃН135ЁуЃЛ
ЃЈ3ЃЉШчЭМ5ЃЌНЋЁїBQCШЦЕуBФцЪБеыа§зЊ90ЁуЃЌЕУЕНЁїBQ'AЃЌСЌНгQQ'ЃЌ
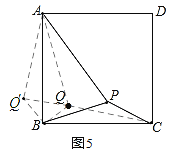
ЁрBQЃНBQ'ЃНbЃЌЁЯQBQ'ЃН90ЁуЃЌЁЯAQ'BЃНЁЯBQCЃН135ЁуЃЌQCЃНAQ'ЃНcЃЌ
ЁрQQ'ЃН![]() bЃЌЁЯBQ'QЃН45ЁуЃЌ
bЃЌЁЯBQ'QЃН45ЁуЃЌ
ЁрЁЯAQ'QЃНЁЯAQ'BЉЁЯBQ'QЃН90ЁуЃЌ
ЁрAQ2ЃНQ'A2+Q'Q2ЃЌ
Ёрa2ЃНc2+2b2ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌЯвABЃЌCDЯрНЛгкЕуEЃЌ
жаЃЌЯвABЃЌCDЯрНЛгкЕуEЃЌ![]() ЃН
ЃН![]() ЃЌЕуDдк
ЃЌЕуDдк![]() ЩЯЃЌСЌНсCOЃЌВЂбгГЄCOНЛЯпЖЮABгкЕуFЃЌСЌНгOAЃЌOBЃЌЧвOAЃН2ЃЌЁЯOBAЃН30Ёу
ЩЯЃЌСЌНсCOЃЌВЂбгГЄCOНЛЯпЖЮABгкЕуFЃЌСЌНгOAЃЌOBЃЌЧвOAЃН2ЃЌЁЯOBAЃН30Ёу
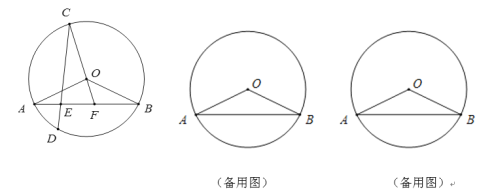
ЃЈ1ЃЉЧѓжЄЃКЁЯOBAЃНЁЯOCDЃЛ
ЃЈ2ЃЉЕБ![]() AOFЪЧжБНЧШ§НЧаЮЪБЃЌЧѓEFЕФГЄЃЛ
AOFЪЧжБНЧШ§НЧаЮЪБЃЌЧѓEFЕФГЄЃЛ
ЃЈ3ЃЉЪЧЗёДцдкЕуFЃЌЪЙЕУ![]() ЃЌШєДцдкЃЌЧыЧѓГіEFЕФГЄЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЃЌШєДцдкЃЌЧыЧѓГіEFЕФГЄЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЪ§бЇаЫШЄаЁзщЕФаЁгБЯыВтСПНЬбЇТЅЧАЕФвЛПУЪїЕФЪїИпЃЌЯТЮчПЮЭтЛюЖЏЪБЫ§ВтЕУвЛИљГЄЮЊ1mЕФжёИЭЕФгАГЄЪЧ0ЃЎ8mЃЌЕЋЕБЫ§ТэЩЯВтСПЪїИпЪБЃЌЗЂЯжЪїЕФгАзгВЛШЋТфдкЕиУцЩЯЃЌгавЛВПЗжгАзгТфдкНЬбЇТЅЕФЧНБкЩЯЃЈШчЭМЃЉЃЌЫћЯШВтЕУСєдкЧНБкЩЯЕФгАИпЮЊ1ЃЎ2mЃЌгжВтЕУЕиУцЕФгАГЄЮЊ2ЃЎ6mЃЌЧыФуАяЫ§ЫувЛЯТЃЌЪїИпЪЧЃЈ ЃЉ
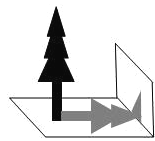
AЁЂ3ЃЎ25m BЁЂ4ЃЎ25m CЁЂ4ЃЎ45m DЁЂ4ЃЎ75m
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
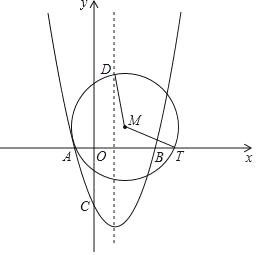
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§yЃНx2+bxЉ3ЕФЭМЯѓгыxжсЗжБ№ЯрНЛгкAЁЂBСНЕуЃЌЕуBЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЌгыyжсЕФНЛЕуЮЊCЃЌЖЏЕуTдкЩфЯпABЩЯдЫЖЏЃЌдкХзЮяЯпЕФЖдГЦжсlЩЯгавЛЖЈЕуDЃЌЦфзнзјБъЮЊ2![]() ЃЌlгыxжсЕФНЛЕуЮЊEЃЌОЙ§AЁЂTЁЂDШ§ЕузїЁбMЃЎ
ЃЌlгыxжсЕФНЛЕуЮЊEЃЌОЙ§AЁЂTЁЂDШ§ЕузїЁбMЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉдкЕуTЕФдЫЖЏЙ§ГЬжаЃЌ
ЂйЁЯDMTЕФЖШЪ§ЪЧЗёЮЊЖЈжЕЃПШєЪЧЃЌЧыЧѓГіИУЖЈжЕЃКШєВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
ЂкШєMTЃН![]() ADЃЌЧѓЕуMЕФзјБъЃЛ
ADЃЌЧѓЕуMЕФзјБъЃЛ
ЃЈ3ЃЉЕБЖЏЕуTдкЩфЯпEBЩЯдЫЖЏЪБЃЌЙ§ЕуMзїMHЁЭxжсгкЕуHЃЌЩшHTЃНaЃЌЕБOHЁмxЁмOTЪБЃЌЧѓyЕФзюДѓжЕгызюаЁжЕЃЈгУКЌaЕФЪНзгБэЪОЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕиНјаажаПМЬхг§ВтЪдЃЌЙцЖЈВтЪдЯюФПЗжЮЊБибЁЯюФПгыздбЁЯюФПЃЌФаЩњздбЁЯюФПЪЧ50УзХм(A)ЁЂСЂЖЈЬјдЖ(B)ЁЂв§ЬхЯђЩЯ(C)ЁЂ1ЗжжгЬјЩў(D)ЃЌУПИіФаЩњвЊдкЫФИіЯюФПГщбЁСНЯюНјааВтЪд.ВтЪдЧАЃЌУПИібЇЩњЯШГщвЛИіЃЌШЗЖЈвЛИіЃЌдйдкЫљЪЃШ§ИіЯюФПжадйГщвЛИі.еХЧПЭЌбЇЕФетЫФИіЯюФПжаЃЌЫћздШЯЮЊ50УзХмИќЩУГЄ.
(1)ШєеХЧПЯШГщЕНСЂЖЈЬјдЖЃЌШЛКѓдйДгЪЃЯТЕФЯюФПжаЫцЛњбЁдёвЛЯюВЮМгВтЪдЃЌдђЫћИеКУбЁжа50УзХмЕФИХТЪЪЧ_______.
(2)ШєеХЧПСЌајЫцЛњГщШЁСНЯюЃЌЧѓЦфжаГщжа50УзХмЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП ШчЭМЃЌдкЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=BCЙ§ЕуCЕФЩфЯпCFНЛБпABгкЕуFЃЌADЁЭCFгкЕуDЃЌBEЁЭCFгкЕуEЃЌAD=3ЃЌBE=1ЃЎ
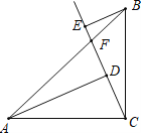
ЃЈ1ЃЉЧѓжЄЃКЁїADCЁеЁїCEBЃЎ
ЃЈ2ЃЉЧѓDEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
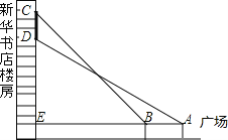
ЁОЬтФПЁПШчЭМЃЌаЁИеЭЌбЇдкЙуГЁЩЯЙлВтаТЛЊЪщЕъТЅЗПЧНЩЯЕФЕчзгЦСФЛCDЃЌЕуAЪЧаЁИеЕФблОІЃЌВтЕУЦСФЛЯТЖЫDДІЕФбіНЧЮЊ30ЁуЃЌШЛКѓЫће§ЖдЦСФЛЗНЯђЧАНјСЫ6mЕНДяBДІЃЌгжВтЕУИУЦСФЛЩЯЖЫCДІЕФбіНЧЮЊ45ЁуЃЌбгГЄABгыТЅЗПДЙжБЯрНЛгкЕуEЃЌВтЕУBE=21mЃЌдђИУЦСФЛЩЯЖЫгыЯТЖЫжЎМфЕФОрРыCDЮЊ______mЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊRtЁїABCЃЌЁЯBACЃН90ЁуЃЌBCЃН5ЃЌACЃН2![]() ЃЌвдAЮЊдВаФЁЂABЮЊАыОЖЛдВЃЌгыБпBCНЛгкСэвЛЕуDЃЎ
ЃЌвдAЮЊдВаФЁЂABЮЊАыОЖЛдВЃЌгыБпBCНЛгкСэвЛЕуDЃЎ
ЃЈ1ЃЉЧѓBDЕФГЄЃЛ
ЃЈ2ЃЉСЌНгADЃЌЧѓЁЯDACЕФе§ЯвжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩюлкЬьКчФГЩЬГЁДгГЇМвХњЗЂЕчЪгЛњНјааСуЪлЃЌХњЗЂМлИёгыСуЪлМлИёШчЯТБэЃК
ЕчЪгЛњаЭКХ | Мз | вв |
ХњЗЂМл(дЊ/ЬЈ) | 1500 | 2500 |
СуЪлМл(дЊ/ЬЈ) | 2025 | 3640 |
ШєЩЬГЁЙКНјМзЁЂввСНжжаЭКХЕФЕчЪгЛњЙВ50ЬЈЃЌгУШЅ9ЭђдЊЃЎ
(1)ЧѓЩЬГЁЙКНјМзЁЂвваЭКХЕФЕчЪгЛњИїЖрЩйЬЈЃП
(2)гЁАдЊЕЉЁБЩЬГЁОіЖЈНјаагХЛнДйЯњЃКвдСуЪлМлЕФЦпЮхелЯњЪлввжжаЭКХЕчЪгЛњЃЌСНжжЕчЪгЛњЯњЪлЭъБЯЃЌЩЬГЁЙВЛёРћ8.5%ЃЌЧѓМзжжаЭКХЕчЪгЛњДђМИелЯњЪлЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com