
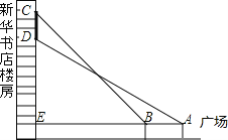
【题目】如图,小刚同学在广场上观测新华书店楼房墙上的电子屏幕CD,点A是小刚的眼睛,测得屏幕下端D处的仰角为30°,然后他正对屏幕方向前进了6m到达B处,又测得该屏幕上端C处的仰角为45°,延长AB与楼房垂直相交于点E,测得BE=21m,则该屏幕上端与下端之间的距离CD为______m.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
|
|
|
|
|
|
|
|
|
|
下列结论:①抛物线的开口向下;②其图象的对称轴为![]() ;③当
;③当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而增大;④方程
的增大而增大;④方程![]() 有一个根大于4;⑤若
有一个根大于4;⑤若![]() ,且
,且![]() ,则
,则![]() .其中正确的结论有( )
.其中正确的结论有( )
A.①②③B.①②③④⑤C.①③⑤D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为△ABC的内心,过点E作MN∥BC交AB于点M,交AC于点N,若AB=7,AC=5,BC=6,则MN的长为( )

A. 3.5B. 4C. 5D. 5.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师要求学生探究如下问题:
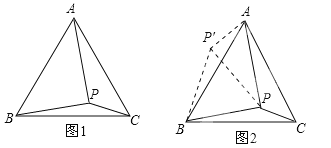
(1)如图1,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,试求∠BPC的度数.李华同学一时没有思路,当他认真分析题目信息后,发现以PA、PB、PC的长为边构成的三角形是直角三角形,他突然有了正确的思路:如图2,将△BPC绕点B逆时针旋转60°,得到△BP′A,连接PP′,易得△P′PB是等边三角形,△PP′A是直角三角形.则∠BPC=_______°.
,PC=1,试求∠BPC的度数.李华同学一时没有思路,当他认真分析题目信息后,发现以PA、PB、PC的长为边构成的三角形是直角三角形,他突然有了正确的思路:如图2,将△BPC绕点B逆时针旋转60°,得到△BP′A,连接PP′,易得△P′PB是等边三角形,△PP′A是直角三角形.则∠BPC=_______°.
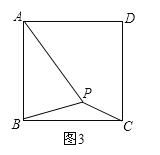
(2)如图3,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1,试求∠BPC的度数.
,PC=1,试求∠BPC的度数.
(3)在图3中,若在正方形ABCD内有另一点Q,QA=a,QB=b,QC=c(a>b,a>c),试猜想a,b,c满足什么条件时,∠BQC的度数与第(2)问中∠BPC的度数相等,请直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在Rt△ABC中,∠C=90°,点O在边BC上,以点O为圆心,OB为半径的圆经过点A,过点A作直线AD,使∠CAD=2∠B.

(1)判断直线AD与⊙O的位置关系,并说明理由;
(2)若OB=4,∠CAD=60°,请直接写出图中弦AB与![]() 围成的阴影部分的面积.
围成的阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上的一动点.连接CE,过点B作BF⊥CE,垂足为F交直线CD于点G.
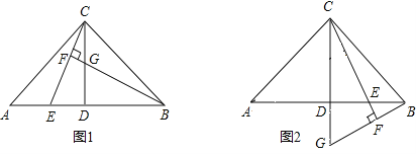
(1)如图l,当点E在线段AD上时,请直接判断AE与CG的数量关系;
(2)如图2,当点E在线段DB上时,(1)中AE与CG的数量关系是否依然成立,若成立,请证明;若不成立,请说明理由.
(3)当AC=2![]() ,且四边形DEFG的面积为
,且四边形DEFG的面积为![]() 时,请直接写出线段AE的长.
时,请直接写出线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
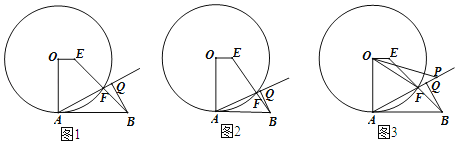
【题目】如图,OA是⊙O的半径,点E为圆内一点,且OA⊥OE,AB是⊙O的切线,EB交⊙O于点F,BQ⊥AF于点Q.
(1)如图1,求证:OE∥AB;
(2)如图2,若AB=AO,求![]() 的值;
的值;
(3)如图3,连接OF,∠EOF的平分线交射线AF于点P,若OA=2,cos∠PAB=![]() ,求OP的长.
,求OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点 A(2,m),B(2,m-5)在平面直角坐标系中,点O为坐标原点.若△ABO是直角三角形,则m的值不可能是( )
A.4B.2C.1D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2018西安国际马拉松”于2018年10月20日在陕西西安举行,该赛事共有三项:![]() .“马拉松”、
.“马拉松”、![]() .“半程马拉松”、
.“半程马拉松”、![]() .“迷你马拉松”小明和小刚有幸参与了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组.
.“迷你马拉松”小明和小刚有幸参与了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组.
(1)小明被分配到“迷你马拉松”项目组的概率为________.
(2)利用列表或树状图求小明和小刚被分配到不同项目组的概率________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com