
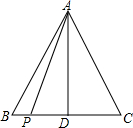
 如图,在△ABC中,AB=AC=2,点P在BC上:
如图,在△ABC中,AB=AC=2,点P在BC上:分析 ①根据勾股定理,可得答案;
②根据勾股定理,可得AB2=AD2+BD2,AP12=AD2+P1D2,根据平方差公式,可得AB2-AP12=BD2-P1D2=(BD+P1D)(BD-P1D)=P1C•BP1,根据等式的性质,可得m2=AB2=AP22+BP2•P2C=4,根据有理数的运算,可得答案.
解答 解:①∵AB=AC,P是BC的中点,
∴AP⊥BC
∴m=AB2=AP2+BP2=AP2+BP•CP=4;
②如图所示: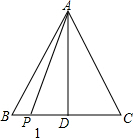
过点A作AD⊥BC于D,
∵AB=AC,
∴BD=CD.
在Rt△ABD中,AB2=AD2+BD2①
在Rt△APD中,AP12=AD2+P1D2②
①-②得:AB2-AP12=BD2-P1D2=(BD+P1D)(BD-P1D)=P1C•BP1,
∴m1=AB2=AP12+BP1•P1C=4,
同理:m2=AB2=AP22+BP2•P2C=4,
m3=AB2=AP32+BP3•P3C
…
m1+m2+…+m2015=4×2015=8060.
故答案为:4,8060.
点评 本题考查了勾股定理,利用了勾股定理,等式的性质,利用平方差公式得出AB2-AP12=BD2-P1D2=(BD+P1D)(BD-P1D)=P1C•BP1是解题关键.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | (-a2)2=-a4 | B. | $\sqrt{3}$+$\sqrt{4}$=2$\sqrt{3}$ | C. | (π-2)0=0 | D. | ($\frac{1}{3}$)-2=9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ① | B. | ①④ | C. | ①③ | D. | ①②④⑥ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由①式得x=$\frac{7}{3}$+4y,再代入②式 | B. | 由②式得y=$\frac{25+10x}{10}$,再代入①式 | ||
| C. | ①×3得③式,再将③式与②式相减 | D. | 由②式得9x=10y-25,再代入①式 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | |
| 甲种货车车辆数(辆) | 5 | 2 |
| 乙种货车车辆数(辆) | 3 | 6 |
| 累计运货数(吨) | 37.5 | 39 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
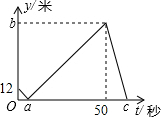 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步300米,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则以下结论:①a=6;②b=88;③c=72,其中正确的结论个数为( )
甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步300米,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则以下结论:①a=6;②b=88;③c=72,其中正确的结论个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com