
我市某区对参加市模拟考试的8000名学生的数学成绩进行抽样调查,抽取了部分学生的数学成绩(分数为整数)进行统计,绘制成频率分布直方图.如下图,已知从左到右五个小组的频数是之比依次是6:7:11:4:2,第五小组的频数是40.
(1)本次调查共抽取了多少名学生?
(2)若72分以上(含72分)为及格,96分以上(含96分)为优秀,那么抽取的学生中,及格的人数、优秀的人数各占所抽取的学生数的百分之多少?
(3)根据(2)的结论,该区所有参加市模拟考试的学生,及格人数、优秀人数各约是多少人?

(1)600;(2)80%,20%;(3)及格人数约为6400人,优秀人数约为1600人.
【解析】
试题分析:(1)因总数一定;故频数的比值就是频率的比值,可得从左到右各小组的频率之比依次是6:7:11:4:2;且频率之和为1;可求得:第五小组的频率,进而求得共抽查的学生人数;
(2)根据频率的计算方法,计算可得;
(3)用样本估计总体,按照求得的比例,计算可得答案.
试题解析:(1)∵从左到右各小组的频数之比依次是6:7:11:4:2,
∴设第一小组的频数为6a,则其它小组的频数依次为7a,11a,4a,2a,
∵第五小组的频数是40,
∴2a=40,
∴a=20,
∴本次调查共抽取的学生数为6a+7a+11a+4a+2a=600(人).
答:本次调查共抽取的学生数为600人.
(2)由(1)知及格学生的人数为480人,优秀学生的人数为120人,
∴它们各占的百分比为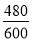 ×100%=80%,
×100%=80%,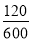 ×100%=20%.
×100%=20%.
答:及格学生的人数,优秀学生的人数各占的百分比为80%和20%;
(3)由(2)知:及格人数为8000×80%=6400(人),
优秀人数为8000×20%=1600(人).
答:8000名学生中,及格人数约为6400人,优秀人数约为1600人.
考点:1.频数(率)分布直方图;2.用样本估计总体.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2013-2014学年浙江省杭州市拱墅区中考二模考试数学试卷(解析版) 题型:解答题
请用直尺和圆规在所给的两个矩形中各作一个不为正方形的菱形,且菱形的四个顶点都在矩形的边上,面积相同的图形视为同一种.(保留作图痕迹).


查看答案和解析>>
科目:初中数学 来源:2013-2014学年河南省驻马店市九年级上学期期末素质测试数学试卷(解析版) 题型:解答题
如图⊙O是∆ABC的外接圆,且AB=AC,点D在弧BC上运动,过点D作DE//BC,DE交AB的延长线于点E,连结AD、BD

(1)求证∠ADB=∠E;
(2)当点D运动到什么位置时,DE是⊙O的切线?请说明理由;
(3)当AB=5,BC=6时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河南省驻马店市九年级上学期期末素质测试数学试卷(解析版) 题型:选择题
二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是()

A.a>0 B.c>0 C.b2-4ac>0 D.a+b+c>0
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河南省中考调考二数学试卷(解析版) 题型:解答题
如图,已知直线AB与x轴、y轴分别交于A和B,OA=4,且OA、OB长是关于x的方程x2﹣mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM并延长交x轴于N.
(1)求⊙M的半径.
(2)求线段AC的长.
(3)若D为OA的中点,求证:CD是⊙M的切线.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年河南省中考调考二数学试卷(解析版) 题型:填空题
如图,先将一平行四边形纸片ABCD沿AE,EF折叠,使点E,B′,C′在同一直线上,再将折叠的纸片沿EG折叠,使AE落在EF上,则∠AEG= 度.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省邯郸市九年级中考二模数学试卷(解析版) 题型:选择题
某公司在甲、乙两地同时销售某种品牌的汽车.已知在甲、乙两地的销售利润y(单位:万元)与销售量x(单位:辆)之间分别满足: ,
, ,若该公司在甲,乙两地共销售15辆该品牌的汽车,则能获得的最大利润为
,若该公司在甲,乙两地共销售15辆该品牌的汽车,则能获得的最大利润为
A.30万元 B.40万元 C.45万元 D.46万元
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期期中模拟考试数学试卷(解析版) 题型:解答题
如图,在直角坐标平面内,O为原点,抛物线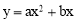 经过点A(6,0),且顶点B(m,6)在直线
经过点A(6,0),且顶点B(m,6)在直线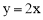 上.
上.
(1)求m的值和抛物线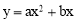 的解析式;
的解析式;
(2)如在线段OB上有一点C,满足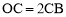 ,在x轴上有一点D(10,0),连接DC,且直线DC与y轴交于点E.
,在x轴上有一点D(10,0),连接DC,且直线DC与y轴交于点E.
①求直线DC的解析式;
②如点M是直线DC上的一个动点,在x轴上方的平面内有另一点N,且以O、E、M、N为顶点的四边形是菱形,请直接写出点N的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com