
【题目】已知二次函数y1=ax2+bx+1(a>0),一次函数y2=x.
(Ⅰ)若二次函数y1的图象与一次函数y2的图象只有一个交点,求a与b之间的关系;
(Ⅱ)在(Ⅰ)的条件下,y1的图象与y2图象的交点为P,且点P的横坐标是2,若将y2向上平移t个单位,与y1交于两点Q,R,△PQR面积为2,求t;
(Ⅲ)二次函数y1图象与一次函数y2图象有两个交点(x1,y1)(x2,y2),且满足x1<2<x2<4,此时设函数y1的对称轴为x=m,求m的范围.
【答案】(1)b2﹣2b+1=4a;(2)t=1;(3)﹣1<m<2.
【解析】
根据二次函数、一次函数、正比例函数的性质,求出交点坐标即可.
解:(1)若二次函数y1的图象与一次函数y2的图象只有一个交点,
即:ax2+bx+1=x,△=(b﹣1)2﹣4a=0,
解得:b2﹣2b+1=4a,…①
答:a与b之间的关系是b2﹣2b+1=4a;
(2)图象如上图所示,若将y2向上平移t个单位后所在直线为PR所在直线为y=x+t![]() ,
,
将P点坐标(2,2)代入二次函数方程得:4a+2b+1=2…②
联立方程①②解得:b=0,a=![]() ,
,
点Q、R的坐标由方程③和二次函数联立得:
![]() x2﹣x+1﹣t=0,则:|xQ﹣xP|=4
x2﹣x+1﹣t=0,则:|xQ﹣xP|=4![]() ,
,
S△PQR=![]() |xQ﹣xP|PH=2,解得:t=1,
|xQ﹣xP|PH=2,解得:t=1,
答:t=1;
(3)![]() ,即:ax2+(b﹣1)x+1=0,
,即:ax2+(b﹣1)x+1=0,
方程有两个根x1<2<x2<4,根据函数得:
![]()
解得:﹣1<﹣![]() <2,
<2,
答:m的范围为﹣1<m<2.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时10海里的速度航行,甲沿南偏西75°方向以每小时10![]() 海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为________海里/小时?
海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为________海里/小时?
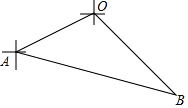
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC.D 是 BC 上一点,且 AD=BD.将△ABD 绕点 A 逆时针旋转得到△ACE.
(1)求证:AE∥BC;
(2)连结 DE,判断四边形 ABDE 的形状,并说明理由.
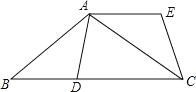
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为5的菱形OABC中,sin∠AOC=![]() ,O为坐标原点,A点在x轴的正半轴上,B,C两点都在第一象限.点P以每秒1个单位的速度沿O→A→B→C→O运动一周,设运动时间为t(秒).请解答下列问题:
,O为坐标原点,A点在x轴的正半轴上,B,C两点都在第一象限.点P以每秒1个单位的速度沿O→A→B→C→O运动一周,设运动时间为t(秒).请解答下列问题:
(1)当CP⊥OA时,求t的值;
(2)当t<10时,求点P的坐标(结果用含t的代数式表示);
(3)以点P为圆心,以OP为半径画圆,当⊙P与菱形OABC的一边所在直线相切时,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】物理兴趣小组20位同学在实验操作中的得分情况如下表:(Ⅰ)求这组数据的众数、中位数;(Ⅱ)求这组数据的平均数;(Ⅲ)将此次操作得分按人数制成如图所示的扇形统计图.扇形①的圆心角度数是多少?
得分(分) | 10 | 9 | 8 | 7 |
人数(人) | 5 | 8 | 4 | 3 |
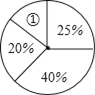
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 A、B是线段MN上的两点,MN4,MA1,MB1.以A为中心顺 时针旋转点M,以B为中心逆时针旋转点N,使MN 两点重合成一点C,构成△ABC,设ABx.(1)则x的取值范围是_________;(2)△ABC的最大面积是_________.
C 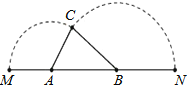
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个二次函数的图象,三位同学分别说出了它的一些特点:
甲:对称轴为直线x=4
乙:与x轴两个交点的横坐标都是整数.
丙:与y轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为3.请你写出满足上述全部特点的一个二次函数解析式__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=-x2+bx+c的部分图象如图所示,A(1,0),B(0,3).
(1)求抛物线的解析式;
(2)结合函数图象,写出当y<3时x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,Rt△OCD的一边OC在x轴上,∠C=90°,点D在第一象限,OC=3,DC=4,反比例函数的图象经过OD的中点A.
(1)求点A的坐标及该反比例函数的解析式;
(2)若该反比例函数的图象与Rt△OCD的另一边DC交于点B,求过A、B两点的直线的解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com