
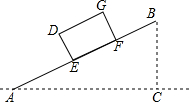
 如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部B处的高BC为8m,A、C在同一水平地面上.
如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部B处的高BC为8m,A、C在同一水平地面上.分析 (1)根据坡度是坡面的铅直高度h和水平宽度l的比计算即可;
(2)作GH⊥AC,根据坡度的概念和矩形的性质以及勾股定理计算即可.
解答 解:(1)∵坡度为i=1:2,BC=8m,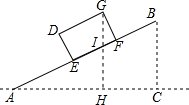
∴AC=8×2=16m;
(2)作GH⊥AC,垂足为H,且与AB相交于I,
∵∠GFI=∠AHI=90°,∠GIF=∠AIH,
∴∠FGI=∠IAH,
∴tan∠FGI=$\frac{1}{2}$,
∵GF=DE=4,
∴FI=2,
∴GI=2$\sqrt{5}$,EI=3,
∴AI=10,
设HI=x,则AH=2x,
∴x2+(2x)2=102,
∴x=2$\sqrt{5}$,即HI=2$\sqrt{5}$,
∴GH=4$\sqrt{5}$m,
答:点G到地面的垂直高度为4$\sqrt{5}$m.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,理解坡度是坡面的铅直高度h和水平宽度l的比是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 相交 | B. | 相切 | ||
| C. | 相离 | D. | 以上三种都有可能 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直角△ACD中,B为AD延长线上一点,且满足AB=CD,在CD上的一点E满足DE=DB,连接BE,F为BE中点,延长AF与过B点的DC的平行线交于点G,连接CG,求证:∠CAG=45°,AD+BG=CG.
如图,直角△ACD中,B为AD延长线上一点,且满足AB=CD,在CD上的一点E满足DE=DB,连接BE,F为BE中点,延长AF与过B点的DC的平行线交于点G,连接CG,求证:∠CAG=45°,AD+BG=CG.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{t}{2}$不是整式 | B. | -2x2y与y2x是同类项 | ||
| C. | $\frac{1}{y}$是单项式 | D. | -3x2y的次数是4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)如图,六边形ABCDEF满足:AB$\stackrel{∥}{=}$EF,AF$\stackrel{∥}{=}$CD.仅用无刻度的直尺画出一条直线l,使得直线l能将六边形ABCDEF的面积给平分;
(1)如图,六边形ABCDEF满足:AB$\stackrel{∥}{=}$EF,AF$\stackrel{∥}{=}$CD.仅用无刻度的直尺画出一条直线l,使得直线l能将六边形ABCDEF的面积给平分;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB=4,点O是线段AB上的点,点C,D分别是线段OA,OB的中点.
如图,AB=4,点O是线段AB上的点,点C,D分别是线段OA,OB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com