
 (1)如图,六边形ABCDEF满足:AB$\stackrel{∥}{=}$EF,AF$\stackrel{∥}{=}$CD.仅用无刻度的直尺画出一条直线l,使得直线l能将六边形ABCDEF的面积给平分;
(1)如图,六边形ABCDEF满足:AB$\stackrel{∥}{=}$EF,AF$\stackrel{∥}{=}$CD.仅用无刻度的直尺画出一条直线l,使得直线l能将六边形ABCDEF的面积给平分;分析 (1)根据平行四边形是中心对称图形,找到对称中心O1、O2,经过O1、O2直线就是所求的直线l.
(2)连接BE交直线l于点K,由△AGO1≌△EKO1得AH=KE,同理KE=CH,由此不难判断结论.
解答 解:(1)直线l如图1所示.
(2)如图2连接BE交直线l于点K.
∵AB∥EF,AB=EF,
∴四边形ABEF是平行四边形,
∴AO1=O1E,BO2=O2D,AF∥BE,
∵AF∥CD,AF=CD,
∴BE∥CD,BE=CD,
∴四边形BCDE是平行四边形,
∵∠O1AG=∠O1EK,∠O1GA=∠O1KE,AO1=O1E
∴△AGO1≌△EKO1,
∴AG=EK,同理EK=CH,
∴AG=CH,GF=HD,故③正确,④错误,
∵AG≠GF,CH≠HD,
∴AG+AB+BC+CH≠GF+EF+DE+DH,
故①②错误.
故答案为③.
点评 本题考查平行四边形的性质、全等三角形的判定和性质,利用平行四边形是中心对称图形找到对称中心是解题的关键.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
 小明不小心敲坏了一块圆形玻璃,于是他拿了其中的一小块到玻璃店去配同样大小的圆形玻璃(如图),店里的师傅说不知圆形玻璃的大小不能配,小明就借了一把尺,先量得其中的一条弦AB的长度为60厘米,然后再量得这个弓形的高CD长度为10厘米,由此就可求得半径解决问题.请你帮小明:
小明不小心敲坏了一块圆形玻璃,于是他拿了其中的一小块到玻璃店去配同样大小的圆形玻璃(如图),店里的师傅说不知圆形玻璃的大小不能配,小明就借了一把尺,先量得其中的一条弦AB的长度为60厘米,然后再量得这个弓形的高CD长度为10厘米,由此就可求得半径解决问题.请你帮小明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
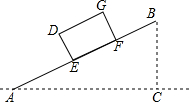 如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部B处的高BC为8m,A、C在同一水平地面上.
如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部B处的高BC为8m,A、C在同一水平地面上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 分类讨论 | B. | 数形结合 | C. | 公理化 | D. | 转化 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com