【题目】小明乘坐一艘游船出海游玩，游船上的雷达扫描探测得到的结果如图所示，每相邻两个圆之间距离是1km（小圆半径是1km），若小艇C在游船的正南方2km，则下列关于小艇A、B的位置描述，正确的是（ ）
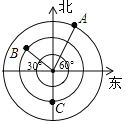
A.小艇A在游船的北偏东60°，且距游船3km
B.游船在的小艇A北偏东60°，且距游船3km
C.小艇B在游船的北偏西30°，且距游船2km
D.小艇B在小艇C的北偏西30°，且距游船2km
53天天练系列答案科目：初中数学 来源： 题型：
【题目】下列说法正确的是（ ）
A.“三角形任意两边之差小于第三边”是必然事件
B.在连续5次的测试中，两名同学的平均分相同，方差较大的同学成绩更稳定
C.某同学连续10次抛掷质量均匀的硬币，6次正面向上，因此正面向上的概率是60%
D.检测某品牌笔芯的使用寿命，适宜用普查
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平行四边形ABCD中，P是AB边上的任意一点，过P点作PE⊥AB，交AD于E，连结CE、CP．已知∠A=60o ．
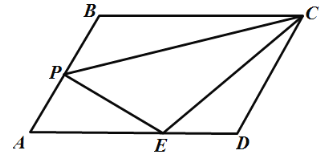
（1）试探究，当△CPE≌△CPB时，CD与DE的数量关系；
（2）若BC=4，AB=3，当AP的长为多少时，△CPE的面积最大，并求出面积的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
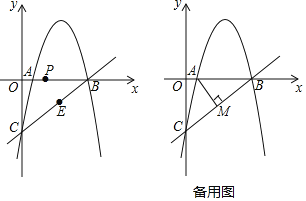
【题目】如图，抛物线
经过x轴上的点A（1，0）和点B及y轴上的点C，经过B、C两点的直线为
．
①求抛物线的解析式．
②点P从A出发，在线段AB上以每秒1个单位的速度向B运动，同时点E从B出发，在线段BC上以每秒2个单位的速度向C运动．当其中一个点到达终点时，另一点也停止运动．设运动时间为t秒，求t为何值时，△PBE的面积最大并求出最大值．
③过点A作
于点M，过抛物线上一动点N（不与点B、C重合）作直线AM的平行线交直线BC于点Q．若点A、M、N、Q为顶点的四边形是平行四边形，求点N的横坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
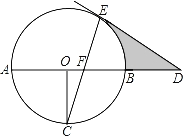
【题目】如图，在⊙O中，AB为⊙O的直径，过O点作OC⊥AB且交⊙O于C点，延长AB到D，过点D作⊙O的切线DE，切点为E，连接CE交AB于F点．
（1）求证：DE＝DF；
（2）若⊙O的半径为2，求CF·CE的值；
（3）若⊙O的半径为2，∠D＝30°，则阴影部分的面积 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
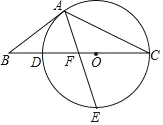
【题目】 如图，点O在△ABC的BC边上，⊙O经过点A、C，且与BC相交于点 D．点E是下半圆弧的中点，连接AE交BC于点F，已知AB＝BF．
（1）求证：AB是⊙O的切线；
（2）若OC＝3，OF＝1，求cosB的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，AB＝3，BC＝4，将对角线AC绕对角线交点O旋转，分别交边AD、BC于点E、F，点P是边DC上的一个动点，且保持DP＝AE，连接PE、PF，设AE＝x（0＜x＜3）．
（1）填空：PC＝ ，FC＝ ；（用含x的代数式表示）
（2）求△PEF面积的最小值；
（3）在运动过程中，PE⊥PF是否成立？若成立，求出x的值；若不成立，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
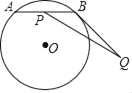
【题目】如图，⊙O上有一个动点A和一个定点B，令线段AB的中点是点P，过点B作⊙O的切线BQ，且BQ=3，现测得
的长度是
，的度数是120°，若线段PQ的最大值是m，最小值是n，则mn的值是（ ）
A. 3
B. 2
C. 9 D. 10
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某学校开展了主题为“垃圾分类，绿色生活新时尚”的宣传活动，为了解学生对垃圾分类知识的掌握情况，该校环保社团成员在校园内随机抽取了部分学生进行问卷调查，将他们的得分按优秀、良好、合格、不合格四个等级进行统计，并绘制了如下不完整的统计表和条形统计图.
等级 | 频数 | 频率 |
优秀 | 20 |
|
良好 | ||
合格 | 10 |
|
不合格 | 5 |
|
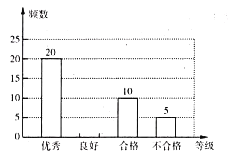
请根据以上信息，解答下列问题：
（1）本次调查随机抽取了______名学生；表中
______，
______；
（2）补全条形统计图；
（3）若全校有2000名学生，请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
