
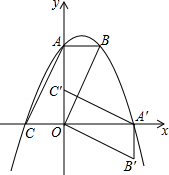
 已知抛物线y=-$\frac{1}{2}$x2+bx+4的对称轴为x=1,与y交于点A,与x轴负半轴交于点C,作平行四边形ABOC并将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′O′C′.
已知抛物线y=-$\frac{1}{2}$x2+bx+4的对称轴为x=1,与y交于点A,与x轴负半轴交于点C,作平行四边形ABOC并将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′O′C′.分析 (1)根据对称轴求出b的值,从而求出二次函数解析式,然后求出A,C的值;
(2)在?ABCD中,∠OAB=∠AOC=90°,则AB∥CO,证出△C′OD∽△BOA,先求出△AOB的周长为6+2$\sqrt{5}$,进而求出△C′OD的周长;
(3)判断此点为费马点,根据公式求出最小值,根据点的坐标求出直线CP的解析式.
解答 解:(1)由已知得,x=-$\frac{b}{2×(-\frac{1}{2})}$=1,则b=1,抛物线的解析式为y=-$\frac{1}{2}$x2+x+4,
∴A(0,4),令y=0,得-$\frac{1}{2}$x2+x+4=0,
∴x1=-2,x2=4.
(2)在?ABCD中,∠OAB=∠AOC=90°,则AB∥CO,
∴OB=$\sqrt{{OA}^{2}+{AB}^{2}}$=2$\sqrt{5}$,OC′=OC=2,
∴∠OC′D=∠OCA=∠B,∠C′OD=∠BOA,
∴△C′OD∽△BOA,
∴$\frac{{C}_{△C′OD}}{{C}_{△BOA}}$=$\frac{OC′}{OB}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,
∵△AOB的周长为6+2$\sqrt{5}$,
∴△C′OD的周长为(6+2$\sqrt{5}$)×$\frac{\sqrt{5}}{5}$=2+$\frac{6\sqrt{5}}{5}$;
(3)此点位费马点,设三角形AOB的三边为a,b,c,
∵OC=2,OA=4,AC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
PA+PB+PC=$\sqrt{\frac{1}{2}\{{a}^{2}+{b}^{2}+{c}^{2}+\sqrt{[3(a+b+c)(a+b-c)(b+c-a)(c+a-b)]}\}}$
=2$\sqrt{4+2\sqrt{2}}$.
直线CP解析式为y=($\sqrt{2}$-1)x+2$\sqrt{2}$-2.
点评 本题是二次函数的综合题型,其中涉及到的知识点有待定系数法求函数解析式,四边形的性质,勾股定理,费马点等知识,综合性强,值得关注.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
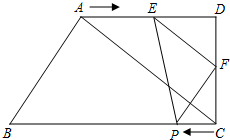 如图,在直角梯形ABCD中,∠D=∠BCD=90°,∠B=60°,AB=$4\sqrt{3}$cm,AD=8cm,直线EF从点A出发沿AD方向匀速运动,速度是2cm/s,运动过程中始终保持EF∥AC,EF交AD于E,交DC于点F;同时,点P从点C出发沿CB方向匀速运动,速度是1cm/s,连接PE、PF,设运动时间为t(s)(0<t<4).
如图,在直角梯形ABCD中,∠D=∠BCD=90°,∠B=60°,AB=$4\sqrt{3}$cm,AD=8cm,直线EF从点A出发沿AD方向匀速运动,速度是2cm/s,运动过程中始终保持EF∥AC,EF交AD于E,交DC于点F;同时,点P从点C出发沿CB方向匀速运动,速度是1cm/s,连接PE、PF,设运动时间为t(s)(0<t<4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
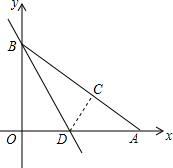 如图,在平面直角坐标系中,点A、B的坐标分别为(8,0)、(0,6),将△OAB折叠,使OB边落在AB边上,点O与点C重合,折痕为BD.
如图,在平面直角坐标系中,点A、B的坐标分别为(8,0)、(0,6),将△OAB折叠,使OB边落在AB边上,点O与点C重合,折痕为BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 经过三个点一定可以作圆 | |
| B. | 同圆或等圆中,相等的圆心角所对的弧相等 | |
| C. | 三角形的外心到三角形各顶点的距离相等 | |
| D. | 经过切点且垂直于切线的直线必经过圆心 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com