练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，四边形ABCD内接于⊙O，AD、BC的延长线相交于点E，AB、DC的延长线相交于点F．若∠E＋∠F＝80°，则∠A＝____°．

    【答案】50

    【解析】试题分析：连结EF，如图，根据圆内接四边形的性质得∠A+∠BCD=180°，根据对顶角相等得∠BCD=∠ECF，则∠A+∠ECF=180°，根据三角形内角和定理得∠ECF+∠1+∠2=180°，所以∠1+∠2=∠A，再利用三角形内角和定理得到∠A+∠AEB+∠1+∠2+∠AFD=180°，则∠A+80°+∠A=180°，然后解方程即可．

    试题解析：连结EF，如图，

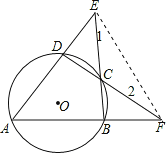
    ∵四边形ABCD内接于⊙O，

    ∴∠A+∠BCD=180°，

    而∠BCD=∠ECF，

    ∴∠A+∠ECF=180°，

    ∵∠ECF+∠1+∠2=180°，

    ∴∠1+∠2=∠A，

    ∵∠A+∠AEF+∠AFE=180°，

    即∠A+∠AEB+∠1+∠2+∠AFD=180°，

    ∴∠A+80°+∠A=180°，

    ∴∠A=50°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】8年级某老师对一、二班学生阅读水平进行测试，并将成绩进行了统计，绘制了如下图表(得分为整数，满分为10分，成绩大于或等于6分为合格，成绩大于或等于9分为优秀)．

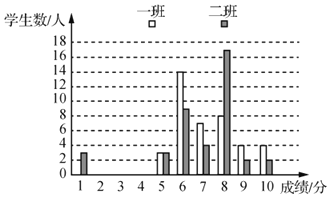
    平均分

    方差

    中位数

    众数

    合格率

    优秀率

    一班

    7.2

    2.11

    7

    6

    92.5%

    20%

    二班

    6.85

    4.28

    8

    8

    85%

    10%

    根据图表信息，回答问题：

    (1)用方差推断， 班的成绩波动较大；用优秀率和合格率推断， 班的阅读水平更好些；

    (2)甲同学用平均分推断，一班阅读水平更好些；乙同学用中位数或众数推断，二班阅读水平更好些．你认为谁的推断比较科学合理，更客观些．为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在相邻两点距离为1的点阵纸上（左右相邻或上下相邻的两点之间的距离都是1个单位长度），三个顶点都在点阵上的三角形叫做点阵三角形，请按要求完成下列操作：

    （1）将点阵△ABC水平向右平移4个单位长度，再竖直向上平移5个单位长度，画出平移后的△A1B1C1；

    （2）连接AA1、BB1，则线段AA1、BB1的位置关系为　 、数量关系为　 ．估计线段AA1的长度大约在　 ＜AA1＜　 单位长度：（填写两个相邻整数）；

    （3）画出△ABC边AB上的高CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，有格点三角形.

    （1）写出三个顶点的坐标.

    （2）将三角形沿方向平移，当点的对应点在轴上时，画出平移后的三角形.

    （3）在给出图形中找一格点（点除外），使三角形与面积相等，并把满足条件的格点用线连起来.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】《人民日报》2019年3月1日刊载了“2018年国民经济和社会发展统计公报”.有关脱贫攻坚的数据如下表.

    年度

    2014

    2015

    2016

    2017

    2018

    农村贫困人口/万

    7017

    5575

    4335

    3046

    1660

    贫困发生率/%

    7.2

    5.7

    4.5

    3.1

    1.7

    （1）在给出图形中，直观表示近年农村贫困人口人数变化情况.

    （2）根据你完善的统计图，写两点你获得的信息.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料：小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如：3+2=（1+）2，善于思考的小明进行了以下探索：

    设a+b=（m+n）2（其中a、b、m、n均为整数），则有a+b=m2+2n2+2mn．

    ∴a=m2+2n2，b=2mn．这样小明就找到了一种把部分a+b的式子化为平方式的方法．

    请你仿照小明的方法探索并解决下列问题：

    （1）当a、b、m、n均为正整数时，若a+b=（m+n）2，用含m、n的式子分别表示a、b，得a=　 　，b=　 　；

    （2）试着把7+4化成一个完全平方式．

    （3）若a是216的立方根，b是16的平方根，试计算：．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题提出：若一个四边形的两组对边乘积之和等于它的两条对角线的乘积，则称这个四边形为巧妙四边形．

    初步思考：（1）写出你所知道的四边形是巧妙四边形的两种图形的名称： ， ．

    （2）小敏对巧妙四边形进行了研究，发现圆的内接四边形一定是巧妙四边形．

    如图①，四边形ABCD是⊙O的内接四边形．

    求证：AB·CD＋BC·AD＝AC·BD．

    小敏在解答此题时，利用了“相似三角形”进行证明，她的方法如下：

    在BD上取点M，使∠MCB＝∠DCA．

    （请你在下面的空白处完成小敏的证明过程．）

    推广运用：如图②，在四边形ABCD中，∠A＝∠C＝90°，AD＝，AB＝，CD＝2．求AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正方形ABCD中，BD是一条对角线，点E在直线CD上（与点C，D不重合），连接AE，平移△ADE，使点D移动到点C，得到△BCF，过点F作FG⊥BD于点G，连接AG，EG．

    （1）问题猜想：如图1，若点E在线段CD上，试猜想AG与EG的数量关系是____________，位置关系是____________；

    （2）类比探究：如图2，若点E在线段CD的延长线上，其余条件不变，小明猜想（1）中的结论仍然成立，请你给出证明；

    （3）解决问题：若点E在线段DC的延长线上，且∠AGF=120°，正方形ABCD的边长为2，请在备用图中画出图形，并直接写出DE的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y=ax2+bx+c (a、b、c为常数且a≠0)中的x与y的部分对应值如下表，

    x

    …

    -3

    -2

    -1

    0

    1

    2

    3

    4

    5

    …

    y

    …

    12

    5

    0

    -3

    -4

    -3

    0

    5

    12

    …

    下列四个结论：

    （1）二次函数y=ax2+bx+c 有最小值，最小值为-3；

    （2）抛物线与y轴交点为（0，-3）；

    （3）二次函数y=ax2+bx+c 的图像对称轴是x=1；

    （4）本题条件下，一元二次方程ax2+bx+c的解是x1=-1,x2=3.

    其中正确结论的个数是（ ）

    A. 4 B. 3 C. 2 D. 1

    查看答案和解析>>

    同步练习册答案