Question

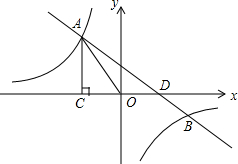
11．如图，已知反比例函数y₁=$\frac{k}{x}$（k＜0）的图象与一次函数y₂=ax+1（a≠0）的图象相交于A、B两点，AC⊥x轴于点C，若△OAC的面积为1，且A点的横坐标为-1．
（1）求反比例函数与一次函数的表达式；
（2）直接写出B点的坐标，并结合图象指出当x为何值时，反比例函数y₁的值小于一次函数y₂的值．

Answer 1

分析 （1）根据反比例函数系数k的几何意义可求出k的值，然后根据条件可求出点A的坐标，然后运用待定系数法就可解决问题；
（2）只需通过解反比例函数与一次函数的表达式组成的方程组，就可求出点B的坐标，然后运用数形结合的思想，结合图象就可解决问题．

解答 解：（1）∵点A在y₁=$\frac{k}{x}$（k＜0）的图象上，S_△OAC=1，
∴$|\begin{array}{l}{k}\end{array}|$=2×1=2．
∵k＜0，∴k=-2，
∴反比例函数的表达式为y₁=-$\frac{2}{x}$．
∵A点的横坐标为-1，
∴当x=-1时，y₁=2，
∴A（-1，2）．
∵点A在y₂=ax+1（a≠0）的图象上，
∴2=-a+1，∴a=-1，
∴一次函数的表达式为y₂=-x+1；

（2）解方程组$\left\{\begin{array}{l}{y=-\frac{2}{x}}\\{y=-x+1}\end{array}\right.$，
得$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$，
∴点B的坐标为（2，-1）．
观察图象可知，当x＜-1或0＜x＜2时，
反比例函数y₁的值小于一次函数y₂的值．

点评 本题主要考查了反比例函数系数k的几何意义、运用待定系数法求一次函数的表达式、反比例函数与一次函数的图象的交点坐标等知识，运用数形结合的思想是解决第（2）小题的关键．