
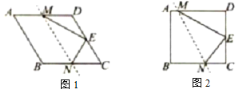
【题目】已知菱形纸片ABCD中,![]() ,点E是CD边的中点将该纸片折叠,使点B与点E重合,折痕交AD,BC边于点M,N,连接ME,NE.请从下面A,B两题中任选一题作答,我选择A.如图1,若
,点E是CD边的中点将该纸片折叠,使点B与点E重合,折痕交AD,BC边于点M,N,连接ME,NE.请从下面A,B两题中任选一题作答,我选择A.如图1,若![]() ,则ME的长为______;B.如图2,若
,则ME的长为______;B.如图2,若![]() ,则ME的长为_____.
,则ME的长为_____.
【答案】A.![]() B.
B.![]()
【解析】
(1)连接BD,BE,则△BCD是等边三角形,则BE⊥CD,由BE⊥MN,得到MN∥CD,则∠BNM=∠NCE=∠ENM=60°,得到△CNE是等边三角形,则CN=CE=2,得到N为BC中点,M为AD中点,连接AO,则ME=![]() ,由OD=2,CD=4,利用勾股定理求出CO,即可得到答案;
,由OD=2,CD=4,利用勾股定理求出CO,即可得到答案;
(2)连接BM,由折叠性质,得到BM=EM,在Rt△ABM中,![]() ,在Rt△EDM中,
,在Rt△EDM中,![]() ,设
,设![]() ,则
,则![]() ,根据等量关系,即可求出
,根据等量关系,即可求出![]() ,然后求出ME的长度.
,然后求出ME的长度.
解(1)如图,连接BD,BE,AC,
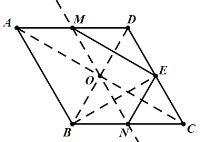
在菱形ABCD中,∠NCE=∠BAD=60°,BC=CD,
∴△BCD是等边三角形,
∵点E是CD中点,
∴BE⊥CD,
由折叠的性质,得到BE⊥MN,
∴MN∥CD,
∴∠BNM=∠NCE=∠ENM=60°,
∴∠ENC=∠NCE=∠NEC=60°,
∴△CNE是等边三角形,
∴CN=CE=2,
∴点N是BC的中点,
∴点M是AD的中点,
∴ME=![]() ,
,
∵在Rt△ODC中,![]() ,CD=4,
,CD=4,
由勾股定理,得![]() ,
,
∴ME=![]() ;
;
故答案为:![]() .
.
(2)如图,连接BM,
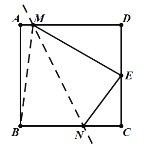
由折叠的性质,得BM=EM,
∵∠A=90°,则四边形ABCD是正方形,
∴∠D=∠A=90°,AB=AD=4,
在Rt△ABM和Rt△EDM中,由勾股定理,得:
![]() ,
, ![]()
设![]() ,则
,则![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴AM=![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】甲,乙两人分别从![]() ,
,![]() 两地相向而行,甲先走3分钟后乙才开始行走,甲到达
两地相向而行,甲先走3分钟后乙才开始行走,甲到达![]() 地后立即停止,乙到达
地后立即停止,乙到达![]() 地后立即以另一速度返回
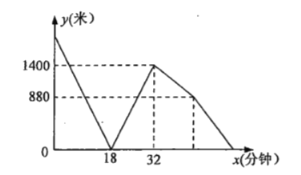
地后立即以另一速度返回![]() 地,在整个行驶的过程中,两人保持各自速度匀速行走,甲,乙两人之间的距离
地,在整个行驶的过程中,两人保持各自速度匀速行走,甲,乙两人之间的距离![]() (米)与乙出发的时间
(米)与乙出发的时间![]() (分钟)的函数关系如图所示.当甲到达
(分钟)的函数关系如图所示.当甲到达![]() 地时,则乙距离
地时,则乙距离![]() 地的时间还需要________分钟.
地的时间还需要________分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东坡商贸公司购进某种水果成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价P(元/kg)与时间t(天)之间的函数关系式P=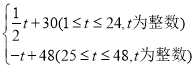 且其日销售量y(kg)与时间t(天)的关系如表下:
且其日销售量y(kg)与时间t(天)的关系如表下:
时间t(天) | 1 | 3 | 6 | 10 | 20 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | … |
(1)已知y与t之间的变化符合一次函数关系,试求在第30天的日销售量.
(2)哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售前24天中,该公司决定每销售1kg水果就捐赠n元利润(0<n<9)给“精准扶贫”对象,现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个小风筝与一个大风等形状完全相同,它们的形状如图所示,其中对角线AC⊥BD.已知它们的对应边之比为1:3,小风筝两条对角线的长分別为12cm和14cm.
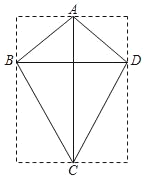
(1)小风筝的面积是多少?
(2)如果在大风筝内装设一个连接对角顶点的十字交叉形的支撑架,那么至少需用多长的材料?(不记损耗)
(3)大风筝要用彩色纸覆盖,而彩色纸是从一张刚好覆盖整个风筝的矩形彩色纸(如图中虚线所示)裁剪下来的,那么从四个角裁剪下来废弃不用的彩色纸的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD中,![]() ,点E是BC边上的一点(不与B,C重合),以BE为边构造菱形BEFG,使点G落在AB的延长线上,连接BD,GE,射线FE交BD于点H.
,点E是BC边上的一点(不与B,C重合),以BE为边构造菱形BEFG,使点G落在AB的延长线上,连接BD,GE,射线FE交BD于点H.
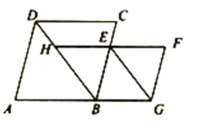
(1)求证:四边形BGEH是平行四边形;
(2)请从下面AB两题中任选一题作答,我选择______题.
A.若四边形BGEH为菱形,则BD的长为_____.
B.连接HC,CF,BF,若![]() ,且四边形BHCF为矩形,则CF的长为______.
,且四边形BHCF为矩形,则CF的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴的负半轴相交于点C(如图),点C的坐标为(0,﹣3),且BO=CO.
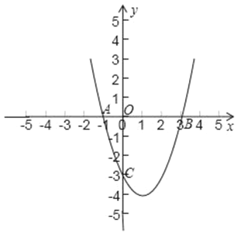
(1)求出B点坐标和这个二次函数的解析式;
(2)求△ABC的面积;
(3)设这个二次函数的图象的顶点为M,求AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线型拱桥,当拱顶离水面8m时,水面宽AB为12m.当水面上升6m时达到警戒水位,此时拱桥内的水面宽度是多少m?
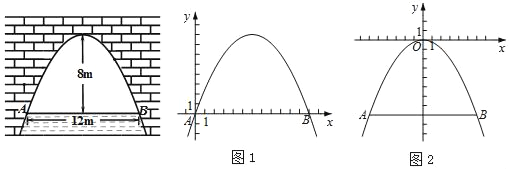
下面给出了解决这个问题的两种方法,请补充完整:
方法一:如图1,以点A为原点,AB所在直线为x轴,建立平面直角坐标系xOy,
此时点B的坐标为( , ),抛物线的顶点坐标为( , ),
可求这条抛物线所表示的二次函数的解析式为 .
当y=6时,求出此时自变量x的取值,即可解决这个问题.
方法二:如图2,以抛物线顶点为原点,对称轴为y轴,建立平面直角坐标系xOy,
这时这条抛物线所表示的二次函数的解析式为 .
当y= 时,求出此时自变量x的取值为 ,即可解决这个问题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com