
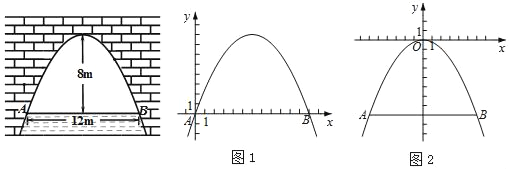
����Ŀ����ͼ�����������ţ���������ˮ��8mʱ��ˮ���ABΪ12m����ˮ������6mʱ�ﵽ����ˮλ����ʱ�����ڵ�ˮ������Ƕ���m��
��������˽�������������ַ������벹��������
����һ����ͼ1���Ե�AΪԭ�㣬AB����ֱ��Ϊx�ᣬ����ƽ��ֱ������ϵxOy��
��ʱ��B������Ϊ���� ������ �����������ߵĶ�������Ϊ���� ������ ������
������������������ʾ�Ķ��κ����Ľ���ʽΪ�� ����
��y��6ʱ�������ʱ�Ա���x��ȡֵ�����ɽ��������⣮
����������ͼ2���������߶���Ϊԭ�㣬�Գ���Ϊy�ᣬ����ƽ��ֱ������ϵxOy��
��ʱ��������������ʾ�Ķ��κ����Ľ���ʽΪ�� ����
��y���� ��ʱ�������ʱ�Ա���x��ȡֵΪ�� �������ɽ��������⣮
���𰸡�12��0��6��8��y����![]() x2+
x2+![]() x��y����
x��y����![]() x2����2����3��
x2����2����3��
��������
����һ�������������ʿɵó�B��O���꣬Ȼ������κ����Ľ���ʽΪy��a��x��6��2��8�ٽ�B��������뼴�ɵõ�a��ֵ.
������������κ����Ľ���ʽΪy��ax2��B����뼴�ɵõ�a��ֵ����y����2ʱ���������ʽ���������.
�⣺����һ��B��12��0����O��6��8����
����κ����Ľ���ʽΪy��a��x��6��2��8��
��B����������ã�a����![]() ��
��
����κ����Ľ���ʽΪy����![]() x2��
x2��![]() x��
x��
������������κ����Ľ���ʽΪy��ax2��
��B��6����8������ã�a����![]() ��
��
����κ����Ľ���ʽΪy����![]() x2��
x2��
y����2ʱ�������ʱ�Ա���x��ȡֵΪ��3��
�ʴ�Ϊ��12��0��6��8��y����![]() x2��
x2��![]() x��y����
x��y����![]() x2����2����3��
x2����2����3��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
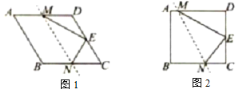
����Ŀ����֪����ֽƬABCD�У�![]() ����E��CD�ߵ��е㽫��ֽƬ�۵���ʹ��B���E�غϣ��ۺ۽�AD��BC���ڵ�M��N������ME��NE.�������A��B��������ѡһ��������ѡ��A.��ͼ1����
����E��CD�ߵ��е㽫��ֽƬ�۵���ʹ��B���E�غϣ��ۺ۽�AD��BC���ڵ�M��N������ME��NE.�������A��B��������ѡһ��������ѡ��A.��ͼ1����![]() ����ME�ij�Ϊ______��B.��ͼ2����
����ME�ij�Ϊ______��B.��ͼ2����![]() ����ME�ij�Ϊ_____.
����ME�ij�Ϊ_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��x2+2x��48
��2��2x2��4x��5��0
��3��sin60��+cos230����![]() tan45��
tan45��
��4��![]() ��3tan60��������1��0+
��3tan60��������1��0+![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
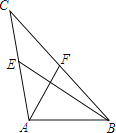
����Ŀ���¶��壺���ǰ����������ഹֱ�������γ�Ϊ���д�����������ͼ��ʾ����ABC��AF��BE�����ߣ���AF��BE������ΪP������ABC�����������γ�Ϊ���д����������������ABE��30����AB��6����ô��ʱAC�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
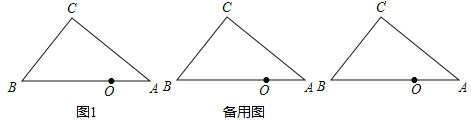
����Ŀ����ͼ����Rt��ABC�У���C��90����AC��4��BC��3��O��AB��һ�㣬��AO��2��
��1�����O��ֱ��AC�ľ���OH�ij���
��2����P�DZ�AC��һ�����㣬��PQ��OP���߶�BC��Q������B��C�غϣ�����AP��x��CQ��y������y����x�ĺ�������ʽ����д��������
��3���ڣ�2���������£���APΪ����ʱ��ʹ��OPQ����CPQ���ƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=2x��˫����y=![]() �ڵ�һ���Ľ���ΪA������A��AB��x����B������ABO�Ƶ�O��ת90�㣬�õ���A��B��O�����A�������Ϊ�� ��
�ڵ�һ���Ľ���ΪA������A��AB��x����B������ABO�Ƶ�O��ת90�㣬�õ���A��B��O�����A�������Ϊ�� ��
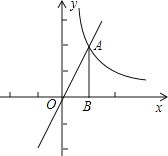
A����1��0��
B����1��0����1��0��
C����2��0����0����2��
D������2��1����2����1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��2��a+1��x+a2+3��0������ʵ����x1��x2
��1����ʵ��a��ȡֵ��Χ
��2����������ABC�����߳��ֱ�Ϊx1��x2��6�����ABC���ܳ�
��3���Ƿ����ʵ��a��ʹx1��x2ǡ��һ���߳�Ϊ![]() �����ε������Խ��ߵij��������ڣ����������ε�������������ڣ�˵�����ɣ�
�����ε������Խ��ߵij��������ڣ����������ε�������������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����5��10��Ͷ�����д�����ͼ
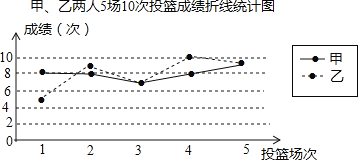
��1�������
ƽ���� | ���� | ��λ�� | ���� | |
�� | ______ | 8 | 8 | ______ |
�� | 8 | ______ | ______ | 3.2 |
��2���ٽ���������5���ɼ���ѡ��ײμ�Ͷ��������������ʲô��
���������Ͷ��1��������8�Σ���ô�ҵ�Ͷ��ɼ��ķ���������仯���������������С��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB��90������OA��OB�ֱ��뷴��������y��![]() ��x��0����y����
��x��0����y����![]() ��x��0����ͼ����A��B���㣬��sin��OAB��ֵ�ǣ�������
��x��0����ͼ����A��B���㣬��sin��OAB��ֵ�ǣ�������

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com