
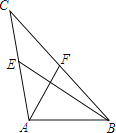
【题目】新定义:我们把两条中线互相垂直的三角形称为“中垂三角形”如图所示,△ABC中AF、BE是中线,且AF⊥BE,垂足为P,像△ABC这样的三角形称为“中垂三角形”,如果∠ABE=30°,AB=6,那么此时AC的长为_____.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】东坡商贸公司购进某种水果成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价P(元/kg)与时间t(天)之间的函数关系式P=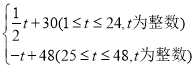 且其日销售量y(kg)与时间t(天)的关系如表下:
且其日销售量y(kg)与时间t(天)的关系如表下:
时间t(天) | 1 | 3 | 6 | 10 | 20 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | … |
(1)已知y与t之间的变化符合一次函数关系,试求在第30天的日销售量.
(2)哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售前24天中,该公司决定每销售1kg水果就捐赠n元利润(0<n<9)给“精准扶贫”对象,现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点.
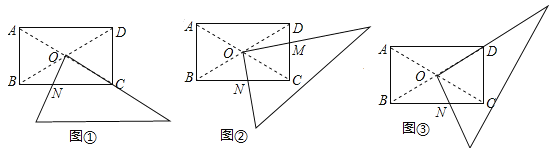
(1)该学习小组成员意外的发现图①中(三角板一边与CC重合),BN、CN、CD这三条线段之间存在一定的数量关系:CN2=BN2+CD2,请你对这名成员在图①中发现的结论说明理由;
(2)在图③中(三角板一直角边与OD重合),试探究图③中BN、CN、CD这三条线段之间的数量关系,直接写出你的结论.
(3)试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,写出你的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过原点的直线与反比例函数![]() 的图象交于
的图象交于![]() 两点,点
两点,点![]() 在第一象限。点
在第一象限。点![]() 在
在![]() 轴正半轴上,连结
轴正半轴上,连结![]() 交反比例函数图象于点
交反比例函数图象于点![]() 。
。![]() 为
为![]() 的平分线,过点
的平分线,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,连结
,连结![]() 。若
。若![]() ,
,![]() 的面积为6,则
的面积为6,则![]() 的值为________。
的值为________。
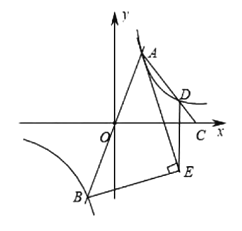
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC中∠BAC的平分线,过A作AE⊥AD交BC的延长线于点E,M为DE的中点.
(1)求证:ME2=MCMB;
(2)如果BA2=BDBE,求证:![]()
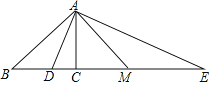
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线型拱桥,当拱顶离水面8m时,水面宽AB为12m.当水面上升6m时达到警戒水位,此时拱桥内的水面宽度是多少m?
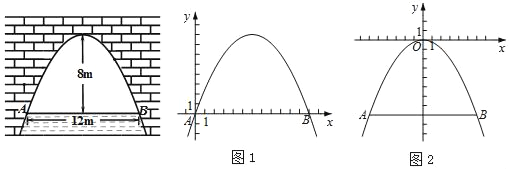
下面给出了解决这个问题的两种方法,请补充完整:
方法一:如图1,以点A为原点,AB所在直线为x轴,建立平面直角坐标系xOy,
此时点B的坐标为( , ),抛物线的顶点坐标为( , ),
可求这条抛物线所表示的二次函数的解析式为 .
当y=6时,求出此时自变量x的取值,即可解决这个问题.
方法二:如图2,以抛物线顶点为原点,对称轴为y轴,建立平面直角坐标系xOy,
这时这条抛物线所表示的二次函数的解析式为 .
当y= 时,求出此时自变量x的取值为 ,即可解决这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).
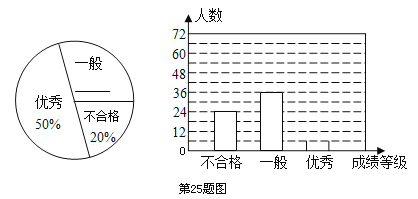
请你根据图中所给的信息解答下列问题:
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有______人达标;
(3)若该校学生有1000人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某一个函数给出如下定义:若存在实数![]() ,对于任意的函数值
,对于任意的函数值![]() ,都满足
,都满足![]() ,则称这个函数是有界函数,在所有满足条件的
,则称这个函数是有界函数,在所有满足条件的![]() 中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.
中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.
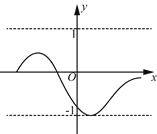
(1)分别判断函数![]()
![]() 和
和![]() 是不是有界函数?若是有界函数,求其边界值;
是不是有界函数?若是有界函数,求其边界值;
(2)若函数![]()
![]() 的边界值是2,且这个函数的最大值也是2,求
的边界值是2,且这个函数的最大值也是2,求![]() 的取值范围;
的取值范围;
(3)将函数![]() 的图象向下平移
的图象向下平移![]() 个单位,得到的函数的边界值是
个单位,得到的函数的边界值是![]() ,当
,当![]() 在什么范围时,满足
在什么范围时,满足![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com